Position and Displacement Vectors
1. Representations of a Position Vector in Plane.
Follow the link: Example 4.4.
2. Three Dimensional Position Vector Magnitude and Direction Cosines.
Follow the link: Example 4.5.
3. Direction of Position Vector from a Direction Cosine Calculation.
Follow the link: Exercise 4.1.3.1.
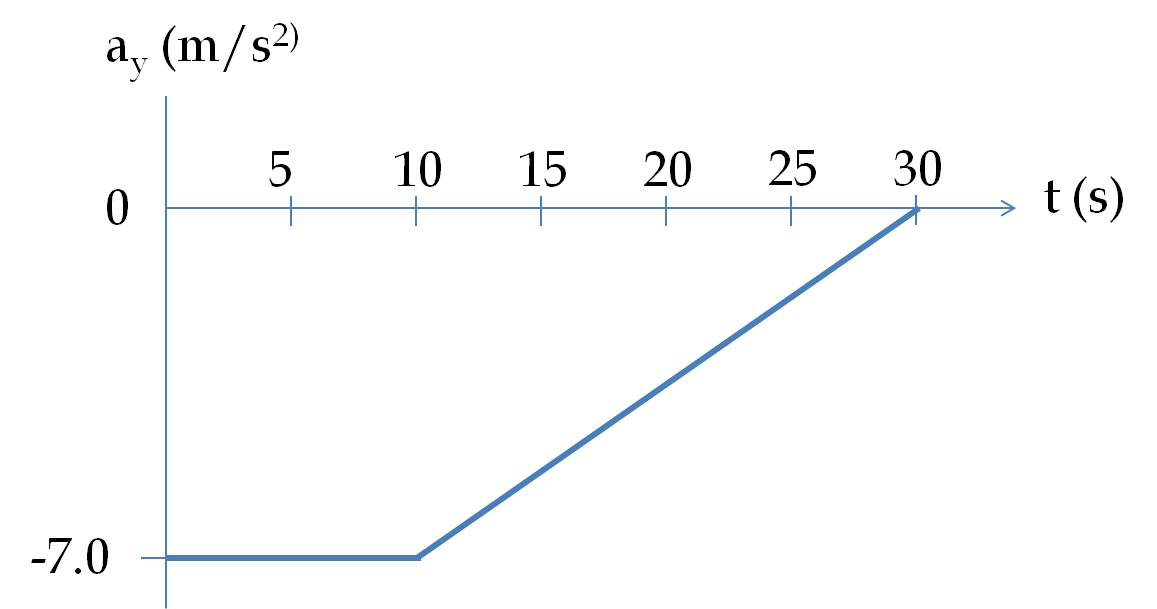
4. Displacement Vector for One-dimensional Motion.
Follow the link: Example 4.10.
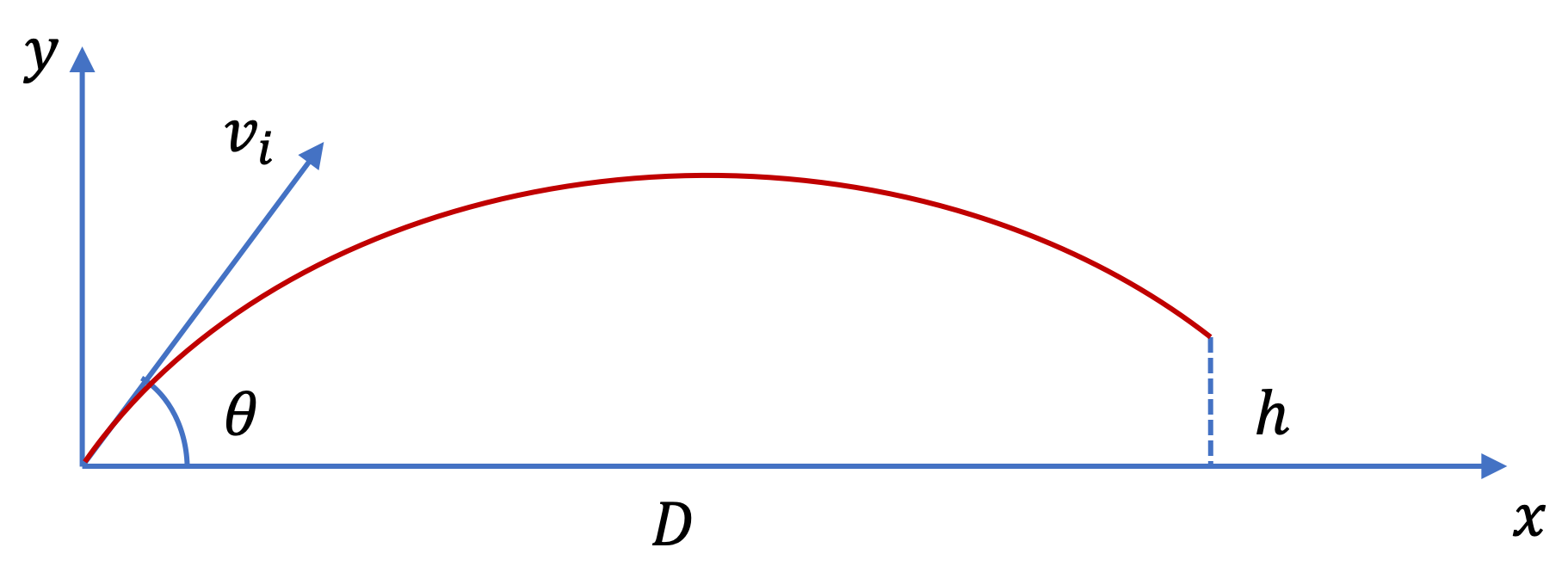
5. Calculating Displacement Vector in a Plane.
Follow the link: Example 4.11.
6. Direction of Displacement Vector in a Plane from Components.
Follow the link: Example 4.12.
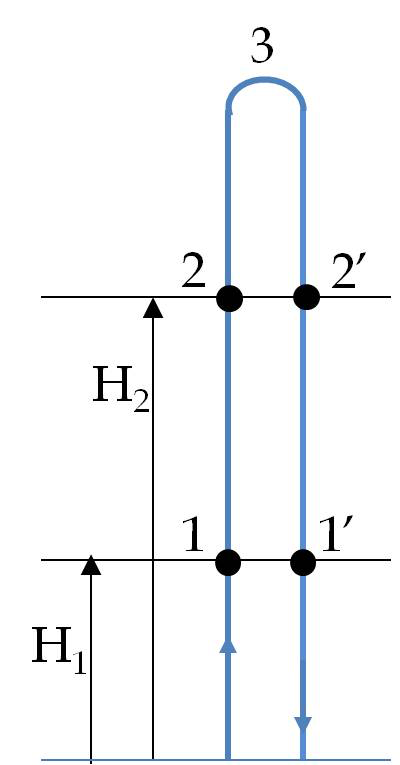
7. Adding Displacement Vectors.
Follow the link: Example 4.13.
8. Finding the Final Position from Initial Position and Displacement.
Follow the link: Exercise 4.2.2.1.
9. Finding the Initial Position from the Final Position and Displacement.
Follow the link: Exercise 4.2.2.2.
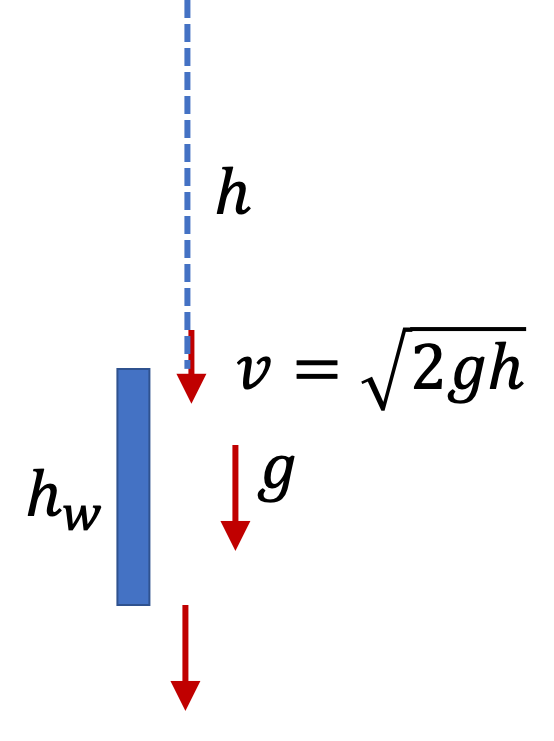
10. Practice with a Friend: How high is the mountain?
Follow the link: Exercise 4.2.2.3.