Example 9.116. A Disk Falling on a Rotating Disk Slowing Down the Disk.
A disk of mass \(M\) and radius \(R\) is rotating at an angular speed \(\omega\) about an axle through its center and vertical to its plane.
Another disk of mass \(M^\prime\) and radius \(R^\prime\) falls on the axle and gets stuck as shown in Figure 9.117.
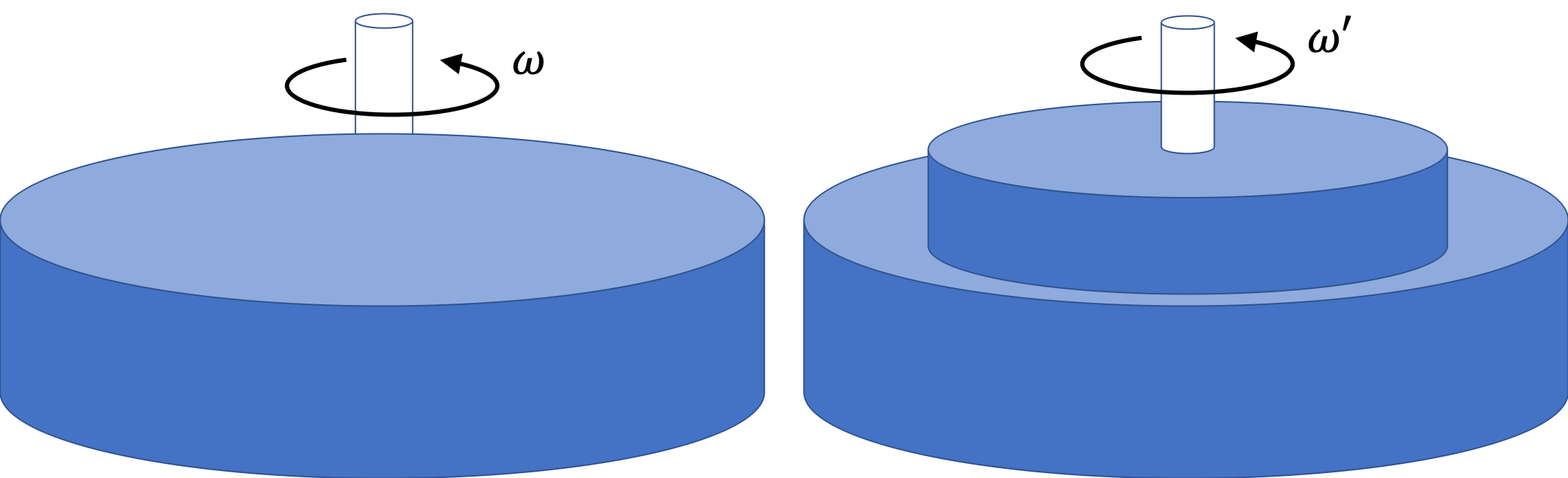
The two rotate at a lower speed \(\omega^\prime\) about the same axis passing through their common center. Find \(\omega^\prime\) in terms of the other quantities given.
Answer.
\(\left( \dfrac{MR^2}{MR^2 + M^\prime {R^\prime}^2}\right)\, \omega\text{.}\)
Solution.
Since the second disk falls along the direction of the rotating disk, its impulse cannot change the angular momentum around the vertical axis. Due to the sticking of the second disk, the moment of inertia after impact will be the sum of the moments of inertia of the two disks. Let us denote the moments of inertia of the two disks aby \(I_1\) and \(I_2\text{.}\)
\begin{equation*}
I_1\, \omega = \left( I_1 + I_2 \right)\, \omega^\prime,
\end{equation*}
where
\begin{equation*}
I_1 = MR^2,\ \ I_2 = M^\prime {R^\prime}^2.
\end{equation*}
Therefore,
\begin{equation*}
\omega^\prime = \left( \dfrac{MR^2}{MR^2 + M^\prime {R^\prime}^2}\right)\, \omega.
\end{equation*}