Sliding/Kinetic Friction

Section 6.12 Sliding/Kinetic Friction

We found above that static friction prevents slide across the surface of contact up to a limit. If you need more static friction to prevent sliding than the maximum static friction \(F_s^{\text{max}}\) possible under the prevailing conditions, then the two body in contact will move relative to each other. This movement is called sliding but resulting acceleration will be less than if there was no friction while it is sliding. This friction is called kinetic friction.

As a concrete example, consider again a book on a table as in Figure 6.51. If the applied force is great enough (before sliding: \(F_\text{applied} \ge F_s^\text{max}\)) the book will start to slide and then you will need some applied force to overcome kinetic friction in order for the book not to slow down and come to rest since kinetic friction will be opposite to the direction of the velocity.

Figure 6.51. Kinetic friction on a book sliding on the table.

While the book is sliding, the molecular bods between the contact surfaces still stretch a little and provide additional attractive force which opposes the sliding motion, but this friction is usually much less than the maximum static friction. The friction when the bodies in contact are sliding past each othre is called the sliding or kinetic friction force. I prefer the term sliding friction, but most books use the term kinetic friction. We will denote kinetic friction force by symbol, \(\vec F_k \) and the magnitude by the same symbol without the arrow.

Just as the normal force, there is no formula for the magnitude of kinetic friction force. The direction of the kinetic friction force on a body is in the opposite direction of the slide. For instance, if book on the table is sliding towards East, the kinetic friction \(\vec F_k \) on the book will be pointed towards West and the corresponding pair force on the table will point towards East.

Although, there is no notion of maximum kinetic friction, the ratio of the magnitude of the kinetic friction \(F_k \) and the normal force is usually somewhat independent of the speed of slide and can be used as a characteristic of that surface. We call this ratio the coefficient of kinetic friction and denote it by \(\mu_k\text{.}\)

\begin{equation} \mu_k = \dfrac{F_k}{F_N}.\tag{6.19} \end{equation}

If you had a ball or a cylinder or a ring, then, you will find that, instead of sliding, it rolls on the other surface. When rolling occurs, we call that friction rolling friction rather than \(kinetic friction\text{.}\) In a rolling motion, the point of contact is actually momentarily at rest. So, rolling friction is a type of static friction. We will discuss rolling friction in another section.

Example 6.52. Kinetic Friction on an Accelerating Book.

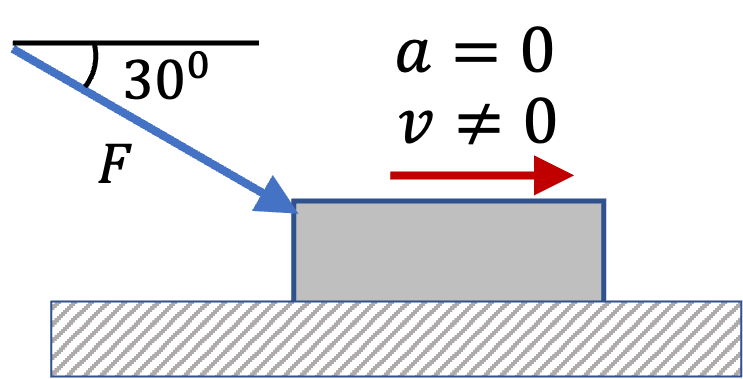
A book of mass \(1.5\text{ kg}\) is at rest on a horizontal table. The book is then pushed with a force at an angle of \(30^{\circ}\) below the horizontal direction. Once the force is increased beyond \(25\text{ N}\text{,}\) the book starts to slide.

At the instant the book starts to slide, we immdiately reduce the force to \(20\text{ N}\) and keep it there for another \(5 \text{ sec}\text{.}\) We find that the book continues to slide during all that time.

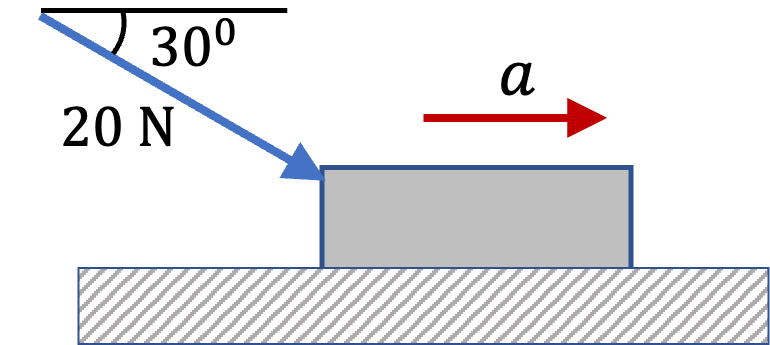
The coefficient of kinetic friction between the book and the table, determined in another experiment, is \(\mu_k = 0.3 \text{.}\)

(a) What is the acceleration of the book when sliding?

(b) How far would the book slide in \(0.5 \text{ sec}\)

Answer.

(a) \(6.59\text{ m/s}^2\) in the horizontal direction towards the positive \(x \) axis, (b) \(1.65\text{ m}\text{,}\) (c) \(0.3\text{ s}\text{.}\)

Solution 1. a

Note that the description of the problem has several numbers that would not be used in solving the problem. They are there to give you a more complete picture of the physical setup of the problem. Below we will follow a systematic way of applying Newton’s laws.

System: the book.

Identify forces on the system:

As usual, we look for contact forces from objects touching the system and long-distance forces, such as gravity, that do not require contact. The following is the list of the forces acting on the system (the book) here by the Agent, the Earth, and the Table. There are two forces from the table - the normal force and the kinetic friction.

Push by an Agent,
Weight of the book by Earth,
Normal force by the Table, and
Kinetic friction by the Table.

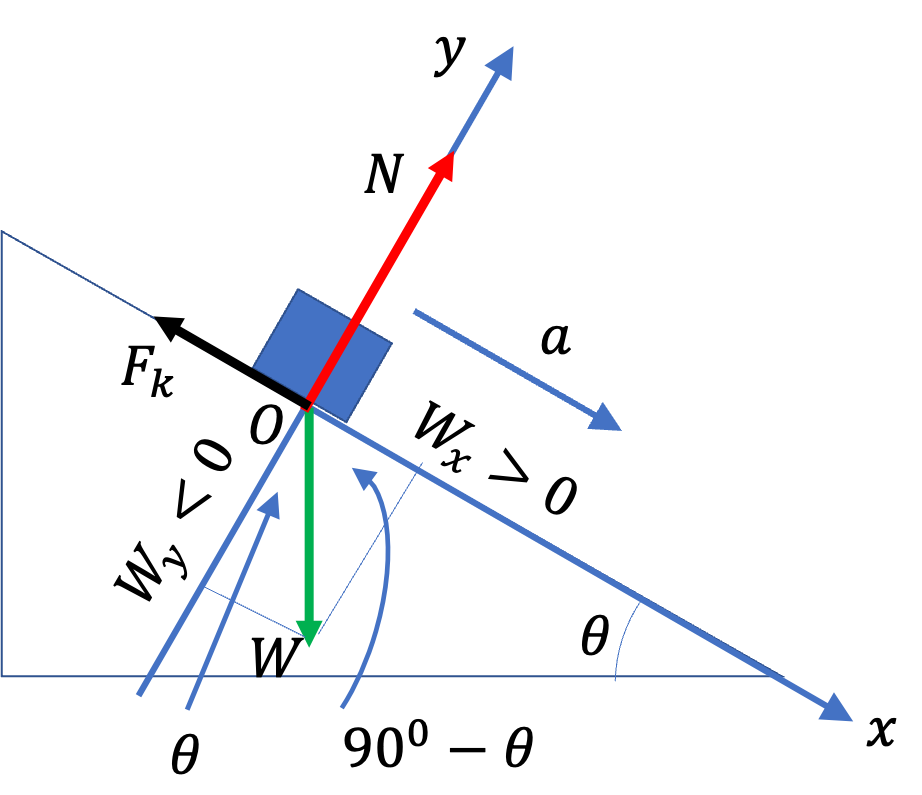
We show the forces in Figure 6.55.

Figure 6.55. Figure for Example 6.52(a).

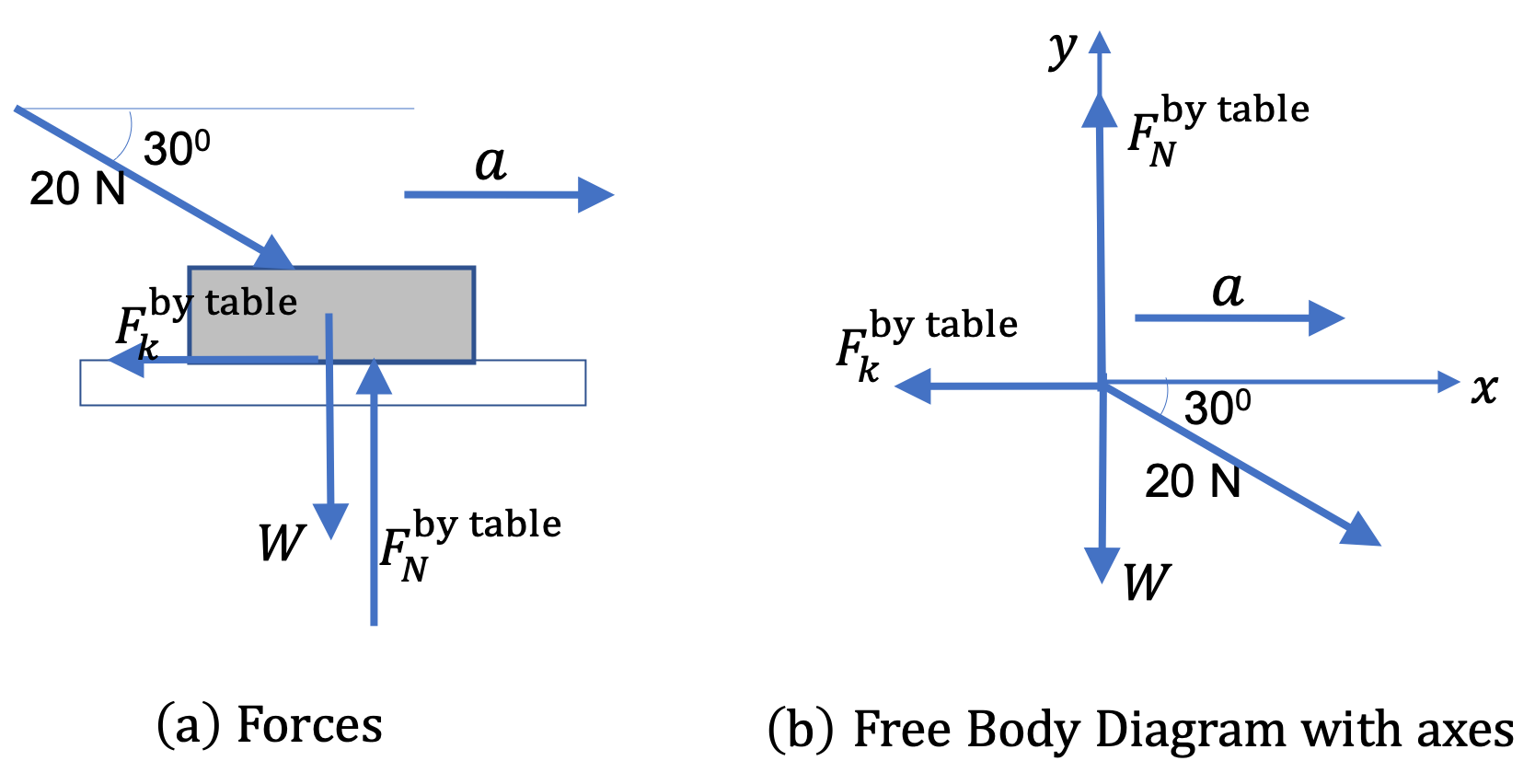
Choose a coordinate system:

Since we expect an axcceleration in the horizontal direction, we pick one of the Cartesian axis, here \(x \) axis, to be in the direction of the accelerations. Let \(a \) be the magnitude of the acceleration, then, the components of the acceleration vector \(\vec a \) is

\begin{equation*} a_x = a,\ \ a_y = 0. \end{equation*}

We will use this when we fill in different quantities in the components of the equation of motion.

Generate equations of motion:

Using the Free-body diagram, we can work out the components of forces.

\begin{align*} \amp \text{Push: } F_x = 20\,\cos\,30^{\circ} = 17.3\text{ N},\ \ F_y = -20\,\sin\,30^{\circ} = -10.0\text{ N},\\ \amp \text{Weight: } W_x = 0,\ \ W_y = - 1.5\times 9.81 = -14.715\text{ N}, \\ \amp \text{Normal from Table: } F_{N,x} = 0,\ \ F_{N,y} = F_N,\\ \amp \text{Kinetic Friction from Table: } F_{k,x} = -F_k,\ \ F_{k,y} = 0, \end{align*}

where the magnitude \(F_k \) can also be written in terms of the magnitude of the normal force \(F_N \text{.}\)

\begin{equation*} F_k = \mu_k F_N \Longrightarrow F_k = 0.3\, F_N. \end{equation*}

Now, we use Cartesian components of forces into the Cartesian components of \(\vec F_{\text{net}} = m\vec a\) to obtain one equation along each axis. We get the following two equations here.

\begin{align*} \amp 17.3 + 0 + 0 - 0.3\, F_N = 1.5\, a,\\ -\amp 10 - 14.715 + F_N + 0 = 0. \end{align*}

Solving equations of motion:

Solving equations of motion gives

\begin{equation*} F_N = 24.715\text{ N},\ \ a= \dfrac{17.3-0.3\times 24.715}{1.5} = 6.59\text{ m/s}^2. \end{equation*}

Interpret the result:

The acceleration of the book when sliding has magnitude \(6.59\text{ m/s}^2\) in the horizontal direction towards the positive \(x \) axis.

Solution 2. b

b We notice that at the instant the book starts to slide, its velocity is zero. And after that, the acceleration is constant along \(x \) axis. Therefore, we can use the kinematics equations for the constant acceleration along the \(x \) axis. Therefore,

\begin{align*} \Delta x \amp = v_{i,x}\, t + \dfrac{1}{2}\,a_x\, t^2,\\ \amp = 0 + \dfrac{1}{2}\times 6.59\times 0.5^2 = 1.65\text{ m}. \end{align*}

Solution 3. c

Using another kinematics equation for constant \(a_x \text{,}\) we get the time to reach the required speed.

\begin{align*} t \amp = \dfrac{v_{f,x} - v_{i,x}}{a_x},\\ \amp = \dfrac{2.0 - 0}{6.59} = 0.3\text{ s}. \end{align*}

Exercises Exercises

1. Kinetic Friction on a Book Sliding With a Constant Velocity.

At the instant the book starts to slide, the book accelerates with increasing speed. The applied force is then reduced to a value such that if we maintain that force, the book just coasts at constant velocity. The coefficient of kinetic friction between the book and the table, determined in another experiment, is \(\mu_k = 0.3 \text{.}\)

What is the magnitude of the applied force for which the book slides at a constant velocity?

Hint.

Solve \(\vec F_{\text{net}} = 0\text{.}\)

Answer.

\(6.17\text{ N} \)

Solution.

This is the same problem as Example 6.52, except we now have zero acceleration, and instead of finding acceleration, we need to find the magnitude of the applied force.

Let \(F \) denote the magnitude of the applied force. Following the same procedure as in the previous example, we find the following equations of motion.

\begin{align*} \amp F\,\cos\,30^{\circ} + 0 + 0 - 0.3\, F_N = 0,\\ -\amp F\,\sin\,30^{\circ} - 14.715 + F_N + 0 = 0. \end{align*}

Multiplying the second equation by 0.3, adding the two equations, and then solving for \(F \text{,}\) we get

\begin{equation*} F = \dfrac{0.3\times 14.715}{ 0.866 - 0.3\times 0.5 } = 6.17\text{ N}. \end{equation*}

2. Motion on an Inclined Plane with Kinetic Friction.

A box is sliding down an smooth board, inclined at an angle of \(30^{\circ} \text{,}\) with increasing speed. Mesurements show that the acceleration down the incline has the magnitude \(3.5\text{ m/s}^2\text{.}\)

Find the coefficient of kinetic friction between the bottom surface of the box and the board. Note: mass is not given on purpose. If you want, you can assume any reasonable number for the mass of the box.

Hint.

Set up \(\vec F = m\vec a \) by identifying all forces on the box. Also, \(x \) axis down the incline is helpful.

Answer.

\(0.165\text{.}\)

Solution.

Developing Ideas for Solution:

Since we want \(\mu_k \text{,}\) this means we need the ratio of kinetic friction to the normal. We will replace \(F_k \) by \(\mu_k N\) and focus on generating equations of motion where \(\mu_k \) will be present.

The equations of motion will come from setting up the \(\vec F = m\vec a \) equation, which starts by identifying all forces on the box. With \(x \) axis pointed down the incline, there will be zero for the \(a_y\text{.}\) That will help in calculations.

Identifying Forces, Drawing Free-Body, and Choosing Axes:

Figure 6.58 shows the three forces acting on the box: (1) Weight by Earth, \(W\text{,}\) (2) Normal by the board, \(N \text{,}\) and (3) Kinetic friction by the board, \(F_k\text{.}\) Also shown are the choice of axes. The axes were chosen so that \(\vec a \) has only one non-zero component.

Figure 6.58. Figure for Exercise 6.12.2.

Working out Components and Getting Equations of Motion:

Let \(a \) be the magnitude of accelration. The components are

\begin{equation*} a_x = a,\ \ \, a_y = 0. \end{equation*}

With this choice of axes, we need to work out the components of only weight. We can migrate angle of incline to the angle of weight with the negative \(y \) axis. When we project the weight vector on the axes, we notice that we must have \(W_x \gt 0\) and \(W_y \lt 0 \text{.}\)

\begin{equation*} W_x = W \, \sin\, \theta,\ \ W_y = - W \, \cos\, \theta. \end{equation*}

Note the minus sign and the trig functions. Make sure you understand how I might have got these.

Now, we can write the \(x \) and \(y\) components of the equation of motion, where we can use \(F_k = \mu_k N\text{.}\)

\begin{align*} \amp W \, \sin\, \theta - \mu_k N = m a, \\ \amp N - W \, \cos\, \theta = 0. \end{align*}

Solving Equations of Motion:

Here, only \(N\) and \(\mu_k \) are unknown. We first get \(N\text{.}\)

\begin{align*} \amp N = mg\, \cos\, \theta, \end{align*}

We then use it in the other equation to get

\begin{align*} \amp mg \, \sin\, \theta - \mu_k \, mg\,\cos\, \theta= m a. \end{align*}

Solving for \(\mu_k \text{,}\) we get

\begin{align*} \amp \mu_k = \dfrac{g \, \sin\, \theta - a}{g\,\cos\, \theta}. \end{align*}

Now, we can put the numbers given.

\begin{align*} \mu_k \amp = \dfrac{g \, \sin\, \theta - a}{g\,\cos\, \theta} \\ \amp = \dfrac{9.81 \, \sin\, 30^{\circ} - 3.5}{9.81\,\cos\, 30^{\circ}} = 0.165. \end{align*}

3. Practice with a Friend: Static Friction Coefficient from a Kinetic Friction Setup.

In Example 6.52, find the value of the coefficient of static friction between the two surfaces.

Answer.

\(0.8\text{.}\)

Prev Top Next