Ampere’s Law

Section 36.4 Ampere’s Law

Ampere’s law states that circulation of magnetic field around a loop is proportional to net current passing through the area within the loop, which we call enclosed current and denote it by \(I_\text{enc}\text{.}\) Specifically,

\begin{equation} \text{Circulation of the } \vec B \text{ field} = \mu_0\, I_\text{enc}.\tag{36.13} \end{equation}

In Calculus language, this is

\begin{equation} \oint_C\, \vec B\cdot d\vec l = \mu_0\, I_\text{enc},\tag{36.14} \end{equation}

where \(C\) is the directed closed path over which the line integral is to be performed. On the right side, the enclosed current can be postive or negative depending on the direction of current as it relates to the direction of loop C. The direction of positive current and loop C are illustrated in Figure 36.44. Note that direction of loop C may or may not be the same as the direction of magnetic field - loop is picked independently of the magnetic field.

A particular emclosed current is positive or negative when included to get the net enclosed current as illustrated in Figure 36.44. When you apply right-hand rule on the direction of the loop, by sweeping your right palm around the loop and positive current in the direction of the thumb; the opposite direction to the thumb is treated as negative.

Figure 36.44. Positive current versus loop direction.

\(I_\text{enc}\) is the net of all positive and negative currents. Figure 36.45 illustrates Ampere’s law for a number of loops.

The loop over which we compute circulation for use in Ampere’s law is called the Amperial loop. This loop is a loop in space and no physical structure, such as wire or anything else need be present at points of the loop. Sometimes we refer to these loops as loops in space or mathematical loop.

Figure 36.45. The value of circulation of magnetic field around Amperian loops can be stated immediately if we know the amount of current enclosed by the loop and the direction from the right-hand-rule applied to the direction of the loop; we do not need to know magnetic field or calculate the circulation integral. In this figure, using Ampere’s law we can state that circulation through loop \(\text{L}_1\) and \(\text{L}_2\) are same, both equal to \(\mu_0 I\text{,}\) circulation through \(\text{L}_3\) is \(-\mu_0 I\text{,}\) which is negative since current through the loop is in the opposite direction of loop, circulation through \(\text{L}_4\) is zero since it has oppositely directed current through the loop which add up to zero, and circulation through \(\text{L}_5\) is zero since no current passes through the loop.

Subsection 36.4.1 (Calculus) Strategy for Using Ampere’s Law

How can we use Ampere’s law to find magnetic field? The statement of Ampere’s law given in Eq. (36.14) shows that the unknown magnetic field is part of the integrand. Therefore, we can use Ampere’s law to calculate magnetic field only in those situations when magnetic field can come out of the integrand.

So, when can \(B\) can come out of integrand of the circulation integral? It turns out that Biot-Savart law (Subsection 36.1.1) helps us make general statements about magnetic field in the case of the three symmetric situations discussed below.

Using Biot-Savart law, it is possible to state direction and distance-dependence functional form of magnetic field, even though calculating the exact formula may be difficult. Once we have these informations, we can choose Amperian loop accordingly, such that on the path chosen, \(\vec B\cdot d\vec l\) is either zero or some constant mgnitude \(B\) times a length.

The three special symmetries that allow these special Amperian loops are

Cylindrical symmetry. This is the case when current is along a long straight wire. Here Amperian loop will be a circle.
Planar symmetry. This is the case if current is on a flat large surface. Here, Amperian loop is a rectangle perpendicular to the surface and passes through the surface.
Solenoidal symmetry. This is the case if current is along \(\hat u_{\phi}\) of cylindrical coordinate. A cylinder that has an insulated wires wound on a cylinder has solenoidal symmetry if the cylinder is long and the area of cross-section is small. Here, Amperian loop is a rectangle that has one side inside and one side outside and runs parallel to the cylinder.

Subsection 36.4.2 (Calculus) Steps in Solving Ampere’s Law Problems

When applying Ampere’s law to find a formula for the magnetic field, we treat \(\vec B\) in the following equation to be the unknown.

\begin{equation*} \oint_{C}\, \vec B\cdot d\vec l = \mu_0 I_\text{encl}. \end{equation*}

Immediately, you should notice that we need to somehow know the closed path \(C\) we will use, and somehow find \(I_\text{enc}\text{.}\) We follow the following four-step process. Notice that calculation is step is way down in the fourth step - without an understanding of steps 1, 2, and 3, just doing calculations is not possible.

Direction of \(\vec B\text{:}\) Using Biot-Savart right-hand rule, guess the direction of \(\vec B\)
Functional form of \(B\text{:}\) Using symmetry guess the functional dependence of magnitude \(B(x,y,z)\text{,}\) i.e., answer the following types of questions: is it a function of \(x\) only, is it a function of \(s=\sqrt{x^2 + y^2}\) only , is it a function of only \(z\text{,}\) etc.
Choosing Amperian Loop: Using the information gathered, we imagine a closed loop, the Amperian loop, that has the following characteristics:
1. Cantain the field point: The Amperian loop passes through the field point of interest,
2. Direction of \(\vec B\) versus direction of loop: \(\vec B\) at every point of the loop is either parallel or antiparallel or perpendicular to the loop direction at that point,
3. \(B\) be a multiple of \(B_P\text{:}\) Magnitdue \(B\) at the field point, \(B_P\) is same either everywhere on the Amperian loop or at finite segments of the loop. In the case of \(B\) not same at all points of the Amperian loop, we require that \(B\) be a multiple of the value at the field points - the mutiplying factor can be zero.
Calculations:
1. Circulation: With Amperian loop chosen, the left side of Ampere’s law turns into a simple product, which can be written as a product of magnitude \(B_P\) and a length \(L\text{,}\) which will have characteristics of the Amperian loop chosen.
  \begin{equation*} \text{Left Side } = B_P L. \end{equation*}
2. \(I_\text{enc}\text{:}\) The right side is computed either directly from the diagram and noting currents crossing the area or by integrating some current density over appropriate cross-section, as you have learned in the chapter on electric currents. For volume current density, \(\vec J\text{,}\) you would integrate over the area of cross-section and for the surface current density, \(\vec K\text{,}\) you will integrate over the line of cross-section.
3. Solve: In all cases, we will get an equation of the following form when we apply Ampere’s law.
  \begin{equation*} B_P L = \mu_0 I_\text{enc}, \end{equation*}
  which immediately gives the magnitude of the field to be
  \begin{equation*} B_P = \dfrac{\mu_0 I_\text{enc}}{L}. \end{equation*}

Example 36.46. (Calculus) Ampere’s Law Application: Magnetic Field of a Steady Current in a Long Thin Wire.

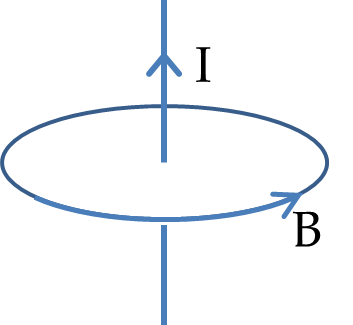
As a first example of application of Ampere’s law for finding magnetic field, we will find the magnetic field at a distance \(s\) from a current \(I\) in infintely long wire. We already know the answer to this problem by applying Biot-Savart Law, but we will re-do this case to explicitly lay out arguments common to all applications of Ampere’s law. Just to recall the answer.

\begin{align*} \amp \text{Magnitude, } B = \dfrac{\mu_0}{2\pi}\,\dfrac{I}{s}.\\ \amp \text{Direction: Use the right-hand-rule of Biot-Savart Law,} \end{align*}

We want to use Ampere’s law to find this answer. We will follow the four-step process suggested above.

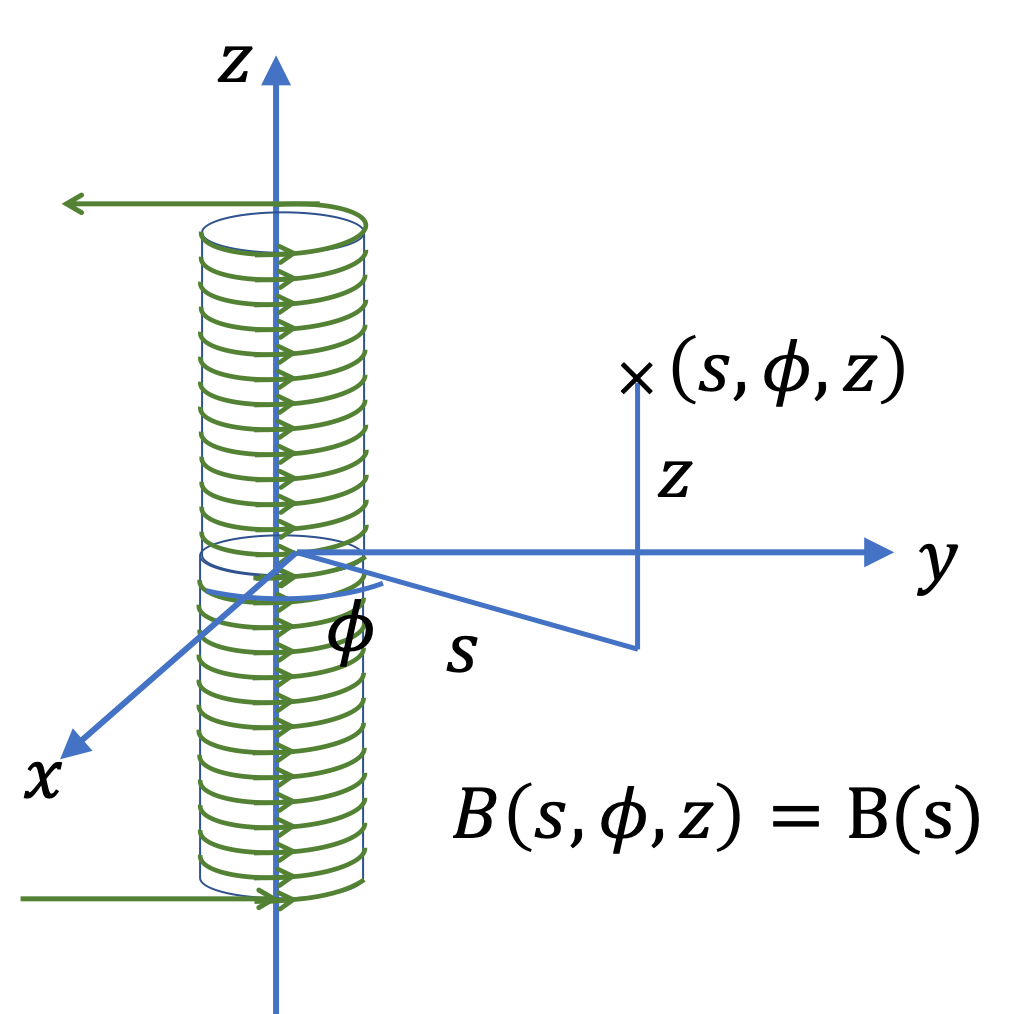
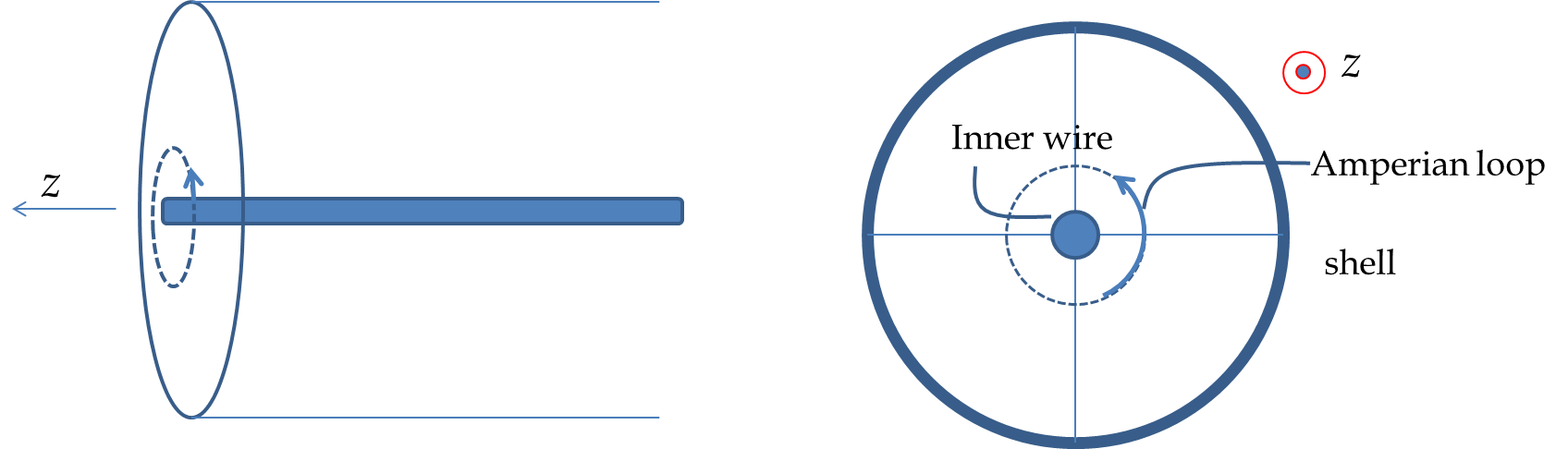
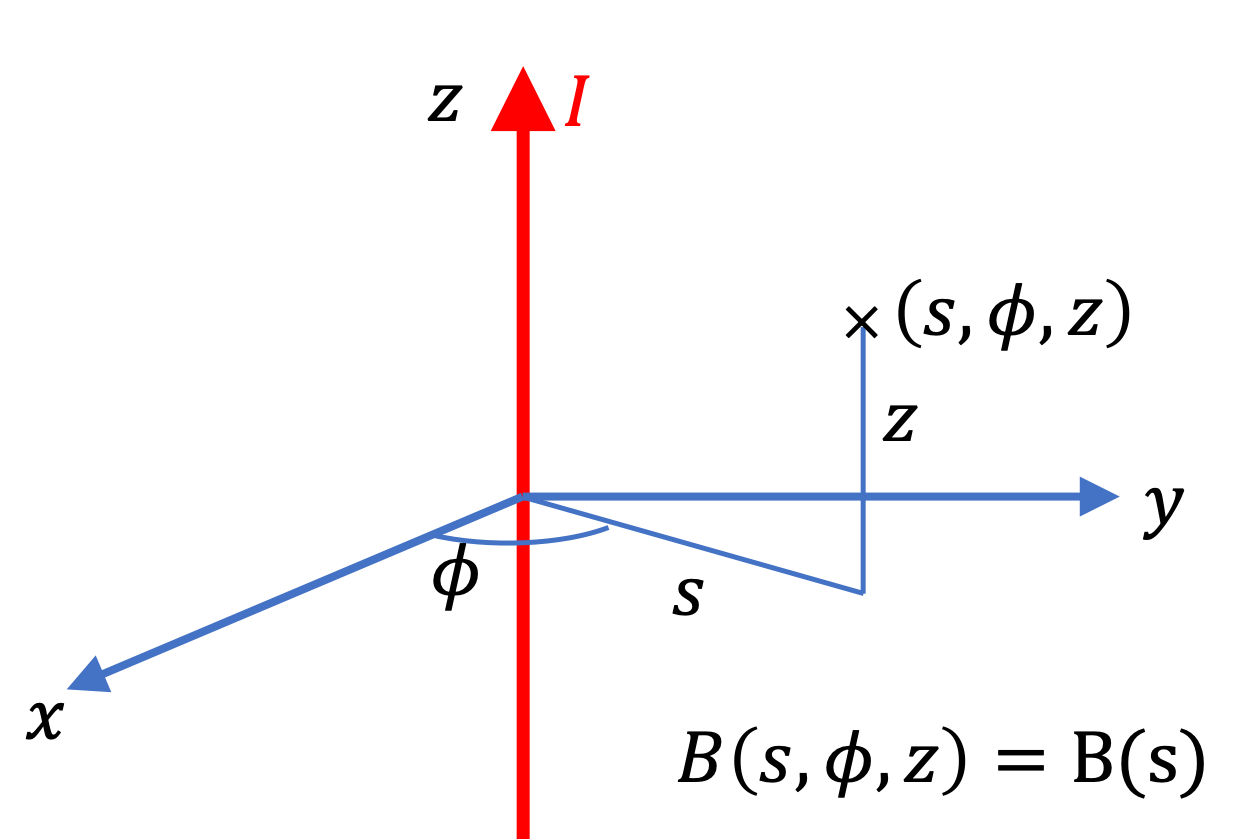
Before we get started, let us look at the current distribution and appropriate coordinate system to use. The current distribution has a cylindrical symmetry. Thereofore, we will use cylindrical coodinate system with coordinates denoted by \((s,\phi, z)\text{.}\) Let current be on the \(z\) axis.

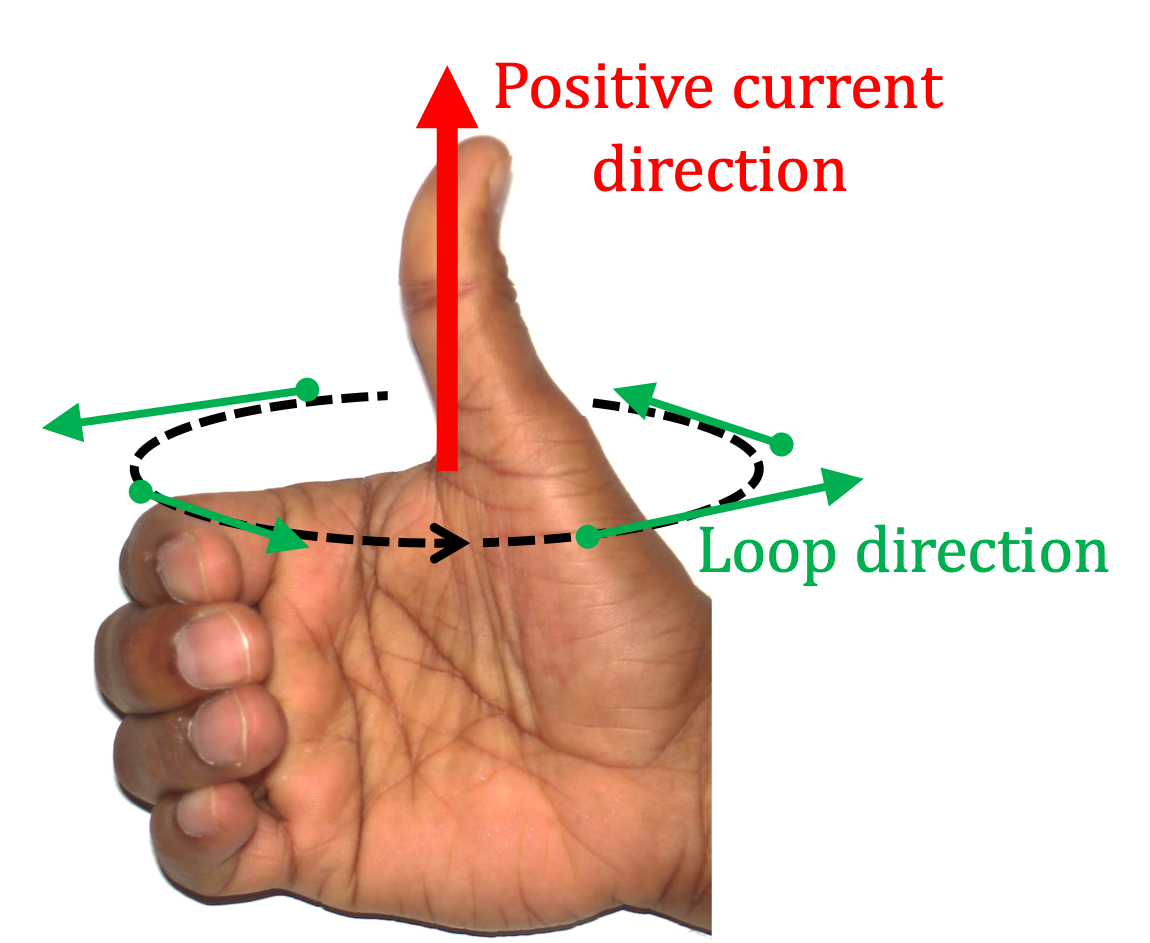
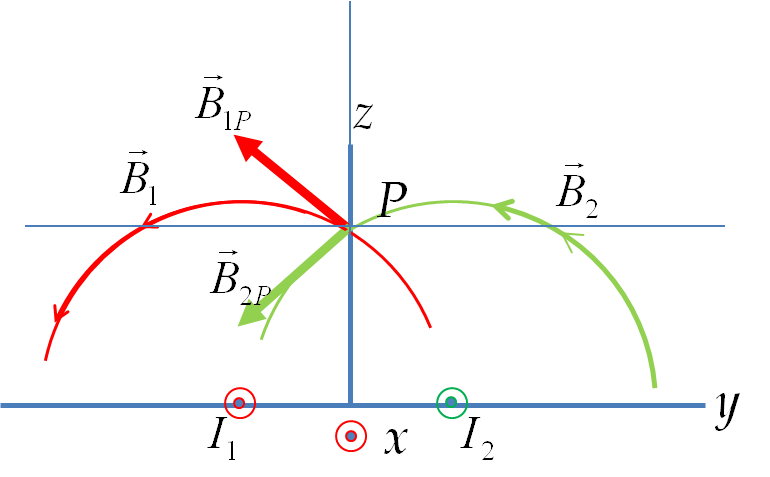
Step 1: What is the direction of magnetic field? Using the Biot-Savart right hand rule, we find that magnetic field will circulate around the wire in circles. At any point it is in the unit vector of cylindrical coordinates, \(\hat u_\phi\) ,direction.

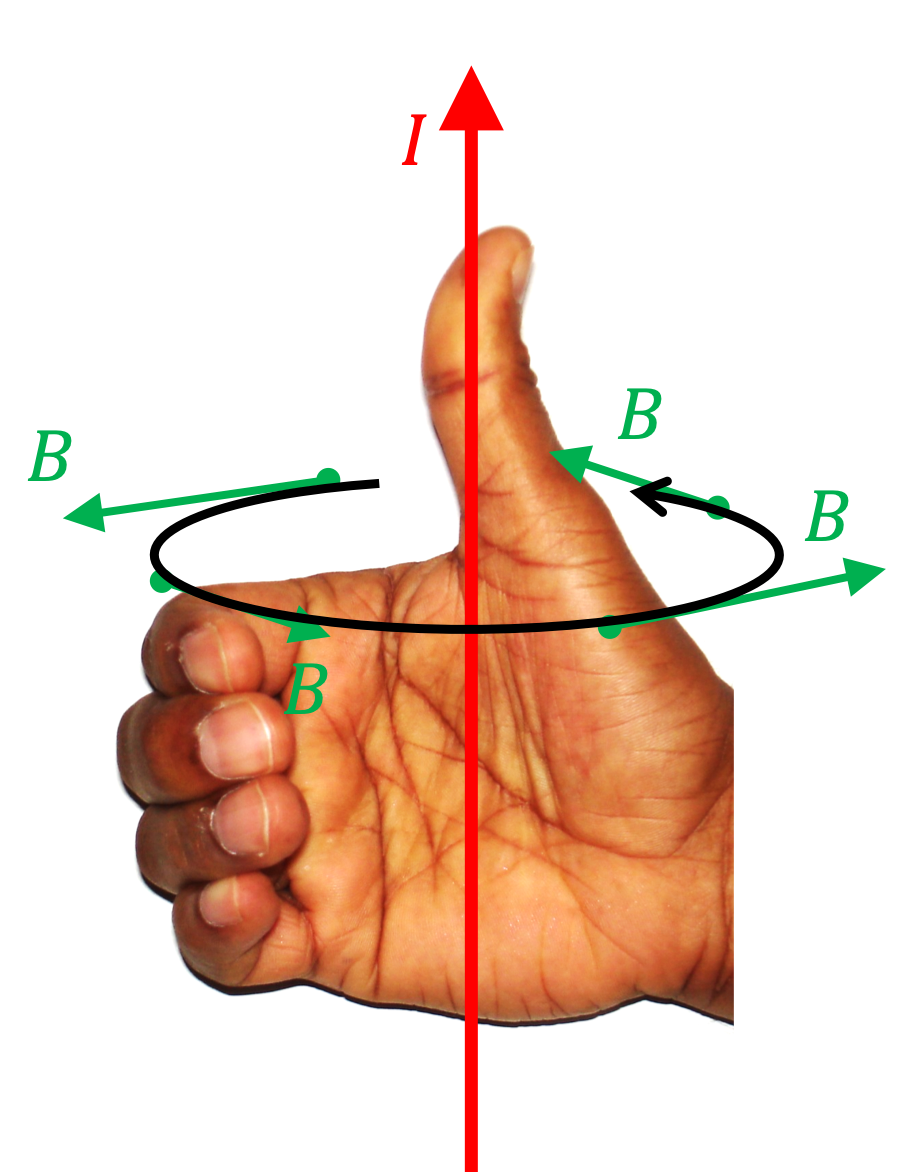
Step 2: What is the functional form of magnitude of the magnetic field? Since current runs on the entire \(z\) axis, nothing can depend on \(z\) coordinate of a point. Also, there is no directional dependence in the current distribution, so, we don’t expect any \(\phi\) dependence. Therefore, we conclude that \(B(s,\phi, z) = B(s)\text{,}\) i.e., only \(s\)-dependent. That means magnitude will be same at all points on a circle centered at the \(z\) axis.

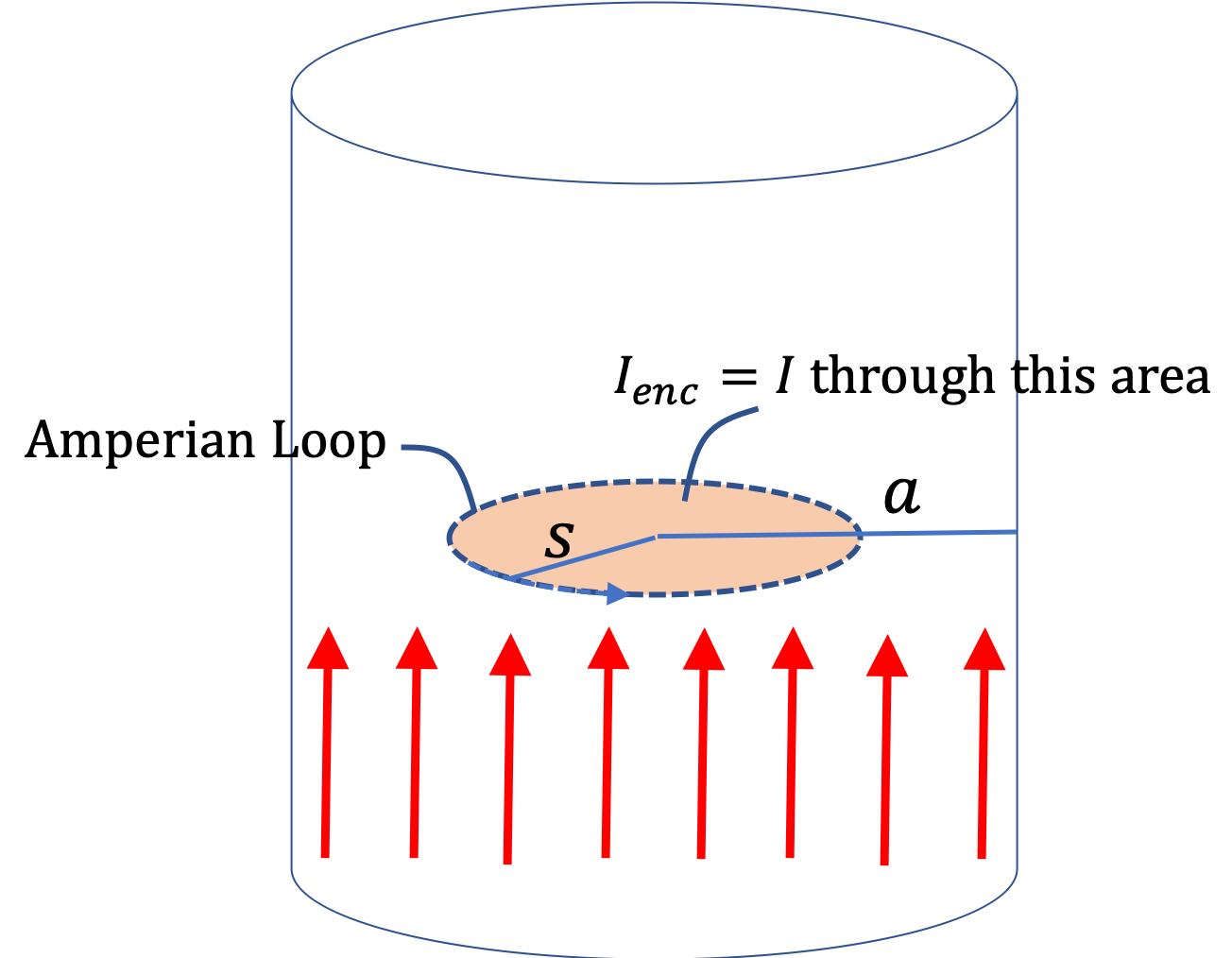
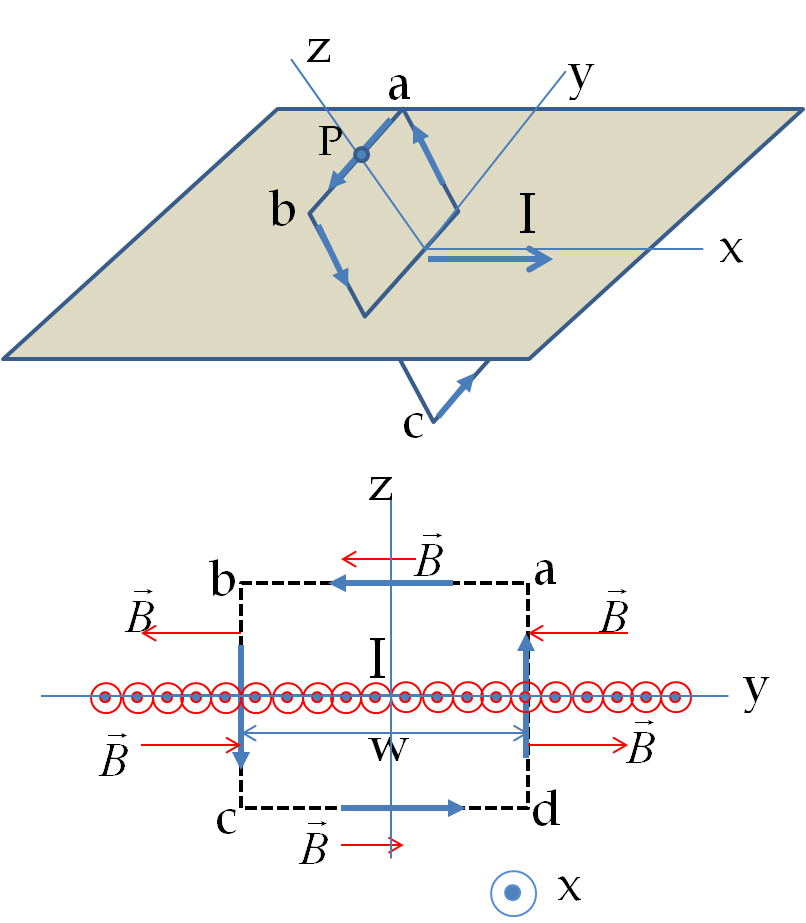
Step 3: Choose Amperian Loop. Let field point P be located at a distance \(s\) from the \(z\) axis. Based on information in steps 1 and 2, if we choose a circle of radius \(s\) with direction \(\hat u_\phi\text{,}\) the magnitude at points of the Amperian loop will be same and the loop direction will be parallel to the field direction.

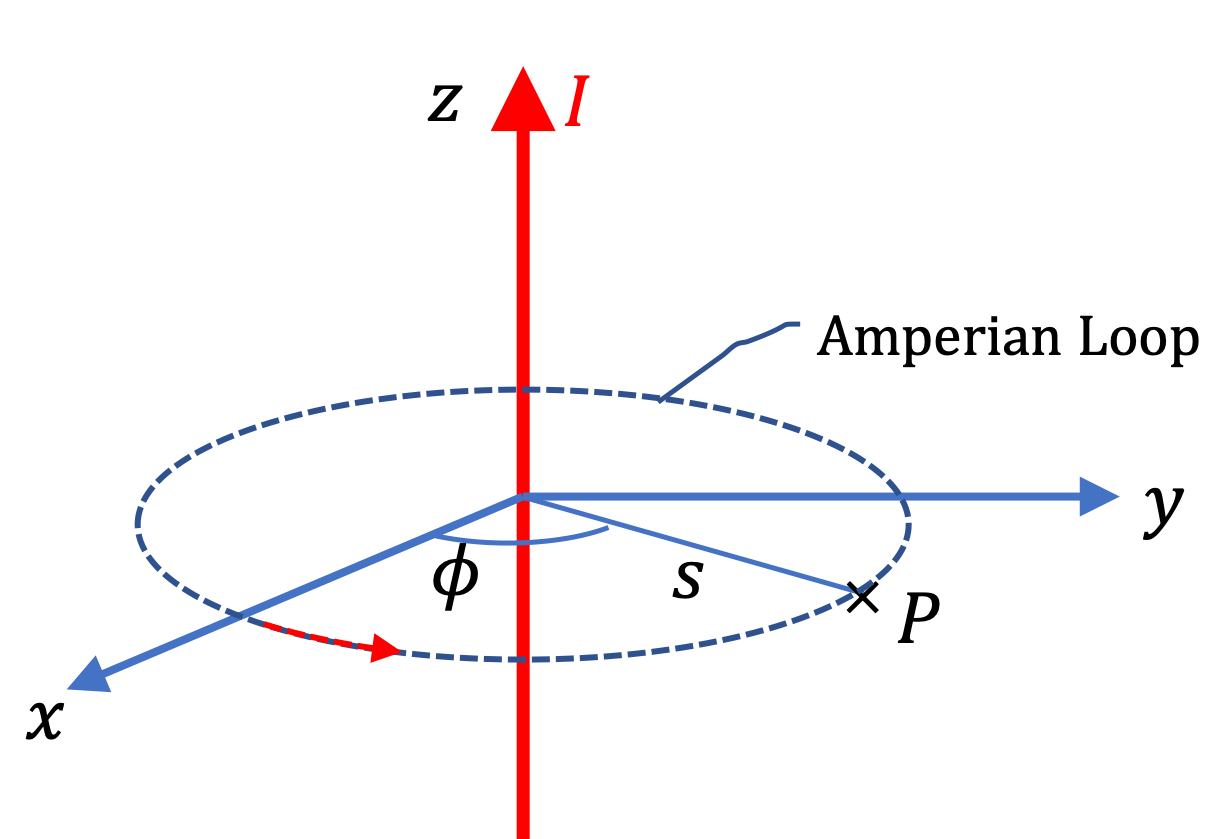
Step 4: Calculations.

We note that \(B=B_P\) at all points of Amperian loop with direction of loop and field parallel. Therefore, left side of Ampere’s law

\begin{equation*} \text{Left side } = 2\pi s B_P. \end{equation*}

For \(I_\text{enc}\) we notice that entire current passes through the loop in the positive current direction, as seen by applying right-hand rule on the loop direction. Therefore,

\begin{equation*} I_\text{enc} = I. \end{equation*}

Using these in Ampere’s law we get

\begin{equation*} 2\pi s B_P = \mu_0, I. \end{equation*}

Therefore, magnitude of magnetic field is

\begin{equation*} B_P = \dfrac{\mu_0}{2\pi}\, \dfrac{I}{s}. \end{equation*}

We have already worked out the direction of the field in step 1 above.

Example 36.47. (Calculus) Ampere’s Law Application: Magnetic Field of a Uniform Steady Current in a Long Thick Wire.

Current \(I \) flows through a thick long wire of radius \(a\text{.}\) Suppose current density is uniformly distributed over the cross-section of the wire. What will be magnetic field at an interior point of the wire?

We will use logic explained in Example 36.46. So, if you have not done that problem yet, you need to go back and familiarize yourself of my techniques.

Let \(s\) be the cylindrical radial coordinate for the field point P. Since P if interest is inside \(s \lt a\text{.}\) Our Amperian loop will be a circle of radius \(s\) as for the thin wire. This will give the following for the left side of Ampere’s law.

\begin{equation*} \text{Left side } = 2\pi s B_P. \end{equation*}

We find \(I_\text{enc}\) by asking: what the the current that flows the Amperian loop? Note, I am not asking what is the current or what is the current in the wire. Since current density is constant this will just be propoetional to the area. The current through the Amperian loop is

\begin{equation*} I_\text{enc} = \dfrac{I}{\pi a^2}\times \pi s^2 = I \dfrac{s^2}{a^2}. \end{equation*}

Using this in Ampere’s law we get

\begin{equation*} 2\pi s B_P = \mu_0 I \dfrac{s^2}{a^2}. \end{equation*}

Therefore, the magnitude of magnetic field at P is

\begin{equation*} B_P = \dfrac{\mu_0}{2\pi a^2} I\,s. \end{equation*}

Note that current increases with cylindrical radial distance while inside the wire. Outside, the formula will be identical to what we found in Example 36.46 since for those points, Amperian loops will include all current in the wire. The direction of the field is obtained in Step 1 by using Biot-Savart right-hand rule.

Example 36.48. (Calculus) Ampere’s Law Application: Magnetic Field of an Ideal Solenoid.

A good way to produce a known constant magnetic field is by an important device called solenoid. You can make a solenoid by tightly winding a platic-coated wire about a cylinder. Suppose, there are \(n\) turns of the wire per unit length. Suppose, you connect the two ends of the wire to a DC-voltage source and wait till current in the wire has stabilized to a value \(I\text{.}\) Let \(R\) be the radius of each coil. Now, we wish to find magnetic field at a point inside the tube and a point outside the tube.

Suppose solenoid is oriented so that its axis is at the \(z\) axis. If we extend the solenoid to \(z=\pm \infty\text{,}\) we will get one aspect of cylindrical symmetry, making expected magnetic field independent of the coordinate \(z\text{.}\) Another aspect is the direction in the \(xy\) plane. If we wind the coils tightly, each turn will be identical to the next and situation in every direction will be same. With this, \(B\) will also be independent of \(\phi\text{.}\)

Therefore, we come to conclusion that magnitude of magnetic field \(B\) can only be a function of the cylindrical radial coordinate \(s\text{.}\)

\begin{equation*} B(s,\phi, z) = B(s). \end{equation*}

Physically, magnetic field should weaken with increasing radial distance from the solenoid axis. So, we expect

\begin{equation} \lim_{s\rightarrow \infty} B(s) = 0.\tag{36.15} \end{equation}

Using Biot-Savart right-hand rule, the direction inside will be towards positive \(z\) axis and outside it would be towards negative \(z\) axis.

(a) For field point outside the loop, the Amperian loop will be a rectangular shape with two sides parallel to axis at radial distanes \(s>R\) and \(s'>s\text{.}\) Then, left side of Ampere’s law gives

\begin{equation*} \text{Left side } = B_P l_\text{ab} + 0 - B(s') l_\text{cd} + 0. \end{equation*}

Here the zeros come from the fact that \(\vec B\) is perpendicular to those sides. The right side of Ampere’s law will be zero since no current goes through this Amperian loop.

Therefore, we get the following equation from Ampere’s law.

\begin{equation*} B_P l_\text{ab} - B(s') l_\text{cd} = 0. \end{equation*}

Let us take the further side at \(s'\) to \(s'=\infty\text{.}\) That will give

\begin{equation*} B_P l_\text{ab} = B(\infty) l_\text{cd} = 0\times l_\text{cd} = 0. \end{equation*}

Therefore,

\begin{equation*} B_P = 0.\text{ (point P outside)} \end{equation*}

We often write this result as

\begin{equation*} B_\text{out} = 0. \end{equation*}

(b) For field point inside the loop, the Amperian loop will be a rectangular shape with two sides parallel to axis at radial distanes \(s\lt R\) and \(s' \gt R\text{.}\) Then, left side of Ampere’s law gives

\begin{equation*} \text{Left side } = B_P l_\text{ab} + 0 - B(s') l_\text{cd} + 0 = B_P l_\text{ab}. \end{equation*}

To obtain the enclosed current, we look at how the wires pierce the Amperian loop area. In each turn, wire carries current \(I\) through the Amperian loop, and all the loops carry current in the same direction. Therefore, current will equal number of turns times \(I\text{.}\)

\begin{equation*} I_\text{enc} = n l_\text{ab}\, I. \end{equation*}

Now, we use Ampere’s law,

\begin{equation*} B_P l_\text{ab} = \mu_0 n l_\text{ab}\, I. \end{equation*}

Therefore,

\begin{equation*} B_P = \mu_0 n \, I.\text{ (point P inside)} \end{equation*}

We often write this result as

\begin{equation*} B_\text{in} = \mu_0 n \, I. \end{equation*}

Example 36.49. Magnetic field of a Planar Surface Current.

Take a large rectangular box and wind a wire with plastic coatings around the box so that on each side we get one layer of wire, with two sides with no wire as shown in the Figure 36.50. What is the magnetic field at a point very close to one of the sides carrying current?

If the point of interest is very close to the surface, we can assume the surface to be infinite and ignore the magnetic field from other surfaces. This gives us a situation of a planar current.

Let the plane of current of interest be the \(xy\)-plane with current towards the positive \(x\)-axis (Figure 36.51). We will use Ampere’s law to find the magnetic field at a point P on the \(z\)-axis at \(z=a\) by following the steps given above.

Step 1: Obtain the direction of \(\vec B_P\text{.}\)

The right-hand rule RHR-II of Biot-Savart law tells us that the magnetic field at point P from currents in different wires on the surface will be in different directions as shown in Figure 36.52.

Figure 36.52. Magnetic field by two currents placed symmetrically about the observation point P. The vector addition of the two magnetic fields will result in a net magnetic field that is pointed along the negative \(y\)-axis. Since every wire has another wire placed symmetrically about point P, the direction of the magnetic field of the planar current is pointed along the negative \(y\)-axis.
First, not that the magnitudes of the magnetic field by the two currents at point P will be equal since point P is same distance from the two wires. Next we notice that the magnetic fields of the two currents \(I_1\) and \(I_2\) cancel each other’s vertical components and only horizontal component is left. This is shown graphically in Figure 36.52.

This cancellation at point P will occur for every pair of current that is symmetrically placed about the point underneath P. Therefore, the direction of the magnetic field at point P will be horizontal towards the negative \(y\)-axis as displayed in Figure 36.52. This argument can be made for any point above the plane since the plane is infinite in extent and placement of the \(z\)-axis is arbitrary. The same argument for points below \(z=0\) would show that the magnetic field there is pointed towards the positive \(z\)-axis.
Step 2: Choose an Amperian loop.

Since, the current is spread over the entire \(xy\)-plane, the magnetic field at arbitrary space point cannot depend on the \(x\) and \(y\) coordinates of the point. Therefore, we expect magnetic field will have the same magnitude at all points in planes \(z = \pm a\text{.}\)

We want to choose an Amperian loop that contains point P and makes use of the constant amplitude planes. A rectangular loop in the \(yz\)-plane, shown as abcda in Figure 36.53, one side of which passes through point P and the other side at \(z=-a\text{,}\) will give circulation that will contain the magnitude of magnetic field at point P.

Figure 36.53. The Amperian loop for a planar current.
Step 3: Deduce an expression for circulation

Let \(w\) denote the lengths of the parallel sides ab and cd. We work out the integral over \(\vec B\cdot d\vec l_A\) on the four straight segments to obtain the circulation around the loop abcda to be

\begin{equation*} \textrm{Circulation:}\ \oint\vec B\cdot d\vec l = B_P w + 0 + B_P w + 0 = 2B_P w, \end{equation*}

where \(0\)’s are for the sides where magnetic field is perpendicular to the loop direction, hence resulting in zero due to the scalar product.
Deduce the amount of enclosed current

The enclosed current is the current through the area of the Amperian loop. Suppose there are \(n\) wires per unit perpendicular distance along the \(y\)-axis. Then, through a distance \(w\) the number of wires will be \(nw\text{,}\) each wire carrying current \(I\text{.}\) Therefore, enclosed current is

\begin{equation*} I_{enc} = n w I. \end{equation*}
Step 5: Solve for magnitude \(B_P\)

Now, we equate the expression of circulation around the Amperian loop to \(\mu_0 I_{enc}\text{.}\) This gives

\begin{equation*} 2B_P w = \mu_0 n w I. \end{equation*}

We now solve this equation for the magnitude of magnetic field at point P.

\begin{equation*} B_P = \frac{\mu_0 n I}{2}. \end{equation*}
Step 6: Write out the magnitude and direction of \(\vec B_P\)

Finally, we write the magnitude and direction of magnetic field at point P can in a compact notation by using the unit vector for the \(y\)-axis, \(\hat u_{y}\text{,}\) since the magnetic field is pointed towards the negative \(y\)-axis. We will need to multiply \(\hat u_{y}\) by minus 1 to get the direction correspond to the negative \(y\)-axis.

\begin{equation} \vec B_P = -\frac{\mu_0 n I}{2} \hat u_y.\tag{36.16} \end{equation}

Further Remarks

This result can also be written using surface current density \(\vec K\) and a unit normal vector \(\hat u_n\) perpendicular to the plane of the current, defined for the direction from the plane of the current towards point P. The surface current density is given by current per unit cross-sectional length. In the present situation since \(n\) is number of wires per unit cross-sectional length and each wire carries a current \(I\) in the direction of the positive \(x\)-axis, the vector surface current density would be

\begin{equation*} \vec K = n I \hat u_x. \end{equation*}

Define the normal direction from plane current towards the field point P. This gives unit normal vector \(\hat u_n\) same as unit vector towards the positive \(z\)-axis.

\begin{equation*} \hat u_n = \hat u_z. \end{equation*}

Equation (36.16) can now be written in a notation that is independent of Cartesian axes as

\begin{equation} \vec B_P = \frac{\mu_0}{2} \vec K\times\hat u_n.\tag{36.17} \end{equation}

This form for the magnetic field is free of reference to a coordinate system.
The magnetic field given by Eq. (36.16) or Eq. (36.17) is independent of the distance to the point P from the plane! The physical situation, however, is somewhat fictitious, since we have ignored the contributions of the wires on other faces that was necessary for the currents to form a closed circuit in the first place. Therefore, in practice, we will not have a constant magnetic field in any realistic arrangement of currents on a cube of finite size. However, our approximation works better as we look at points that are nearer to the center of any one face.

Exercises 36.4.3 Exercises

1. (Calculus) Magnetic Filed of Current in a Coaxial Cable.

Coaxial cables have a conducting wire at the center and a conducting cylindrical shell surroundng the wire separated by a nonconducting material. Current \(I\) in the center wire and the shell run in opposite directions. What is the magnetic field at a point at a distance \(a\) from the center that is located between the the central wire and the the shell?

Hint.

Cylindrical symmetry with only inner wire.

Answer.

\(\dfrac{\mu_0}{4\pi}\,\dfrac{I}{a}\text{.}\)

Solution.

The Amperian loop will be a circle of radius \(a\) with enclosed current will the current in the wire. The current in the shell does not matter for Ampere’s law since it is outside. This problem is same as the problem of a single straight wire. Thus, we can immediately write the answer.

\begin{equation*} B = \dfrac{\mu_0}{2\pi}\,\dfrac{I}{a}. \end{equation*}

The directionn will be obtained by right hand rule and will be either closkwise or counterclockwise around the wire.

2. Circulation of Magnetic Field Using Ampere’s Law.

Find the circulation of magnetic field in terms of currents for the loops shows with dashed lines in various figures using the statement of Ampere’s law.

Solution 1. a

Since current \(I\) passes through the Amperian loop, the circulation around the loop will be either \(+\mu_0\,I\) or \(-\mu_0\,I\text{.}\) We decide the sign by using right-hand-rule around the loop. Here, we find that as we sweep around the loop direction, the thumb points in the direction of the current. Hence, circulation here will be \(+\mu_0\,I\text{.}\)

Solution 2. b

(b) This time the circulation will be negative, \(-\mu_0 I\text{,}\) since, according to the right-had rule, the magnetic field will circulate around the wire in the opposite sense that the direction of the loop in space. (c) 0, (d) 0, (e) \(\mu_0 I\text{.}\)

Solution 3. c

The circulation will be zero since net current included within the area of the loop is \(I-I=0\text{.}\)

Solution 4. d

The circulation will be zero since no current passes through the area of the loop.

Solution 5. d

Answer will be \(+\mu_0\,I\) based on the same logic as in (a).

3. Circulation of Magnetic Field Using Ampere’s Law Ex2.

You find that the circulation of magnetic field around a loop that encloses many wires is zero. From this observation, can you conclude that current is zero in the wires? Explain.

Answer.

No, you cannot conclude that currents in the individual wire are all zero. The circulation will be zero if the net current passing the area attached to the loop is zero - current can pass through the loop in one direction and then cancel out by passing in the opposite direction.

4.

On a flat plate there is a uniform surface current density of \(200\, \text{A/cm}\text{.}\) Determine the magnetic field (both magnitude and direction) 0.5 cm from the surface. For the direction, draw out the surface current and the point at which you have determined the direction of magnetic field.

Answer.

Magnitude: \(12.6\, \text{mT}\text{,}\) Direction: use RHR.

Solution.

The magnetic field of a uniform planar is constant independent of distance from the plane. The magnitude is given by

\begin{align*} B \amp = \dfrac{\mu_0 K}{2} = \dfrac{4\pi\times 10^{-7}\:\textrm{T.m/A}\times 200\:\textrm{A/cm}\times 100\:\textrm{cm/m}}{2}\\ \amp = 1.26\times 10^{-2}\:\textrm{T}. \end{align*}

For the direction we use the right-hand rule of Biot-Savart law. Figure 36.55 shows that if the current in the plane is to the right, then the magnetic field will be out of the page above the plane and into the page below the plane.

5. Surface Current from Magnetic Field using Ampere’s Law.

You need a uniform magnetic field of magnitude \(2.5\, \text{T}\) over a large flat copper surface. Determine the surface current density required. Draw a figure to illustrate the directions of the current and the magnetic field.

Answer.

Magnitude of surface current density: \(4\, \text{MA/m}\text{.}\)

Solution.

We use the magnetic field of current in a plane we have worked out in an example above.

\begin{equation*} B = \dfrac{\mu_0\:K}{2} \end{equation*}

Therefore

\begin{equation*} K = \dfrac{2B}{\mu_0} = \dfrac{2\times 2.5\:\textrm{T}}{4\pi\times 10^{-7}\:\textrm{T.m/A}} = 4\times 10^{6}\:\textrm{A/m}. \end{equation*}

\begin{align*} B \amp \end{align*}

See Figure 36.55 above for the direction of magnetic field and current.

6. Magnetic Field of a Current in a Long Wire Using Ampere’s Law.

A long wire carries a steady current of \(30\,\text{A}\text{.}\) Find the magnitude and direction of magnetic field \(2\, \text{cm}\) from the wire.

Answer.

\(300\,\mu\text{T}\) in the counterclockwise directions when looked from a place where the current would be coming towards the observer.

Solution.

Using the results of magnetic field current in a long wire we find the magnitude of magnetic field as

\begin{align*} B \amp = \dfrac{\mu_0\:I}{2\pi\:r} = \dfrac{4\pi\times 10^{-7}\:\textrm{T.m/A}\times 30\:\textrm{A}}{2\pi\times 0.02\:\textrm{m}} = 3\times 10^{-4}\:\textrm{T}. \end{align*}

The direction is given by the right-hand rule. The magnetic field circulates around the current as shown in Figure 36.56.

7. Magnetic Field of Current in a Coaxial Cable Using Ampere’s Law.

A current in a straight co-axial cable runs in a thin wire at the center and returns at the surface conductor, a cylindrical shell of radius \(0.5\, \text{cm}\text{.}\) For a current of \(3\,\text{A}\text{,}\) determine the magnetic field (a) at a point \(0.2\, \text{cm}\) from the center and (b) at a point \(0.7\, \text{cm}\) from the center.

Answer.

\(3\, \text{mT}\) in the counterclockwise directions when looked from a place so that current in the center wire would be coming towards the observer.

Solution 1. a

We have a cylindrical symmetry for Ampere’s law here. Therefore, we expect the magnetic field to circulate around the axis of the cylinder, which will be taken to be the \(z\)-axis. We choose the Amperian loop to be a circle of radius \(R = 0.2\) cm around the \(z\)-axis and going counter-clockwise when looked from the direction of the positive \(z\)-axis as shown in Figure 36.57.

The only current enclosed by the radius Amperian loop of radius \(r\) = 0.2 cm is the current in the central wire. Looking from the positive \(z\)-axis side, the current in the central wire is coming out and the current in the shell is going in. Therefore, we obtain magnetic field circulating counterclockwise (as seen from the positive \(z\)-axis side) of the magnitude given by

\begin{equation*} B = \dfrac{\mu_0\:I}{2\pi r} = \dfrac{4\pi\times 10^{-7}\:\textrm{T.m/A}\times 3\:\textrm{A}}{2\pi\times 0.002\:\textrm{m}} = 3\times 10^{-4}\:\textrm{T}. \end{equation*}

Solution 2. b

For this point we will choose an Amperian loop of radius \(R = 0.7\) cm. Since no net current passes through the area of this loop we get

\begin{equation*} \oint \vec B \cdot d\vec l = 0. \end{equation*}

By symmetry the magnetic field is constant and either parallel or anti parallel to \(d\vec l\text{.}\) Therefore, this equation becomes

\begin{equation*} \pm\:B\: 2 \pi R= 0, \end{equation*}

where \(R\) is the radius of the loop. Since \(R\ne 0\) we must have \(B = 0\text{.}\)

8. Magnetic Field of Current in a Solenoid and a Wire at Center of Solenoid.

A straight wire at the center of a long solenoid carries \(20\, \text{A}\) current. The solenoid has \(100\) turns per cm and carries \(2\, \text{A}\) current. Find the magnetic field inside the solenoid at a point \(3\, \text{mm}\) from the center, which is outside the thin wire. Assume infinitely long solenoid.

Answer.

\(1.27\, \text{T}\text{,}\) direction \(84^{\circ}\) counter-clockwise from the positive \(x\)-axis towards the positive \(z\)-axis.

Solution.

This problem can be done by superposing the magnetic fields of the currents in the long wire and the solenoid. Let the axis of the solenoid be the \(z\)-axis and the sense of the current in the solenoid be counter-clockwise when observed from the positive \(z\)-axis side.

Suppose also that the current in the long wire at the \(z\)-axis be flowing in the direction of the positive \(z\)-axis. Let us choose the \(x\)-axis so that the point we wish to find the magnetic field lies on the \(x\)-axis at a distance \(r\) on the positive \(x\)-axis.

Now, we are ready to calculate the magnetic field at the field point. The magnetic field of the solenoid will be

\begin{equation*} \vec B_{\textrm{sol}} = \mu_0\:n\:I_{\textrm{sol}}\:\hat u_z, \end{equation*}

and the magnetic field of the current in the long wire will be

\begin{equation*} \vec B_{\textrm{wire}} = \dfrac{\mu_0 \:I_{\textrm{wire}}}{2\pi r}\:\hat u_y. \end{equation*}

The net magnetic field will be a vector sum of the two.

\begin{equation*} \vec B = \dfrac{\mu_0 \:I_{\textrm{wire}}}{2\pi r}\:\hat u_y + \mu_0\:n\:I_{\textrm{sol}}\:\hat u_z \equiv B_y \:\hat u_y + B_z \:\hat u_z. \end{equation*}

Hence, the magnitude of the net magnetic field will be

\begin{equation*} B = \sqrt{B_y^2 + B_z^2}, \end{equation*}

and the direction will be in the \(yz\)-plane, given by the angle \(\tan^{-1}(B_z/B_y)\) with respect to the \(y\)-axis. Putting in the numerical values we obtain

\begin{align*} \amp B_y = \dfrac{4\pi\times 10^{-7}\:\textrm{T.m/A}\times 20\:\textrm{A}}{2\pi\times 0.003\:\textrm{m}} = 1.33\times 10^{-3}\:\textrm{T} \\ \amp B_z = 4\pi\times 10^{-7}\:\textrm{T.m/A}\times 10^4\:\textrm{m}^{-1}\times 1\:\textrm{A} = 1.26\times 10^{-2}\:\textrm{T}. \end{align*}

These values give the net magnetic field at the field point to be approximately \(1.26\times 10^{-2}\) T at an angle \(84^{\circ}\) from the \(y\)-axis towards the positive \(z\)-axis.

9. Magnetic Field of Current in a Solenoid and a Plate.

A long solenoid with \(50\) turns per cm is set parallel to a wide plate that carries a surface current of \(15\, \text{A/cm}\text{.}\) A current of \(1\, \text{A}\) flows in the solenoid such that the solenoid produces magnetic field in the same direction as the direction of flow of the surface current. Find magnetic field at a point inside the solenoid.

Answer.

\(16.35\, \text{mT}\text{,}\) \(82^{\circ}\) from the axis of the solenoid.

Solution.

This problem can be done by superposing the magnetic fields of the currents in the plane and the solenoid. Let the axis of the solenoid be the \(z\)-axis and the sense of the current in the solenoid be counter-clockwise when observed from the positive \(z\)-axis side. This will generate magnetic field pointed towards the positive \(z\)-axis inside the solenoid.

Suppose also that the plane is parallel to \(xz\)-plane as shown in the figure. For concreteness consider an arbitrary point inside the solenoid and take that point to be on the \(x\)-axis as shown. The magnetic field of the the surface current on the plane will be towards the negative \(x\)-axis.

Now, we are ready to calculate the magnetic field at the field point. The magnetic field of the solenoid will be

\begin{equation*} \vec B_{\textrm{sol}} = \mu_0\:n\:I_{\textrm{sol}}\:\hat u_z, \end{equation*}

and the magnetic field of the surface current in the plane will be

\begin{equation*} \vec B_{\textrm{plane}} = - \dfrac{\mu_0 \: K}{2 }\:\hat u_x. \end{equation*}

The net magnetic field will be a vector sum of the two.

\begin{equation*} \vec B = - \dfrac{\mu_0 \: K}{2 }\:\hat u_x + \mu_0\:n\:I_{\textrm{sol}}\:\hat u_z \equiv B_x \:\hat u_y + B_z \:\hat u_z. \end{equation*}

Hence, the magnitude of the net magnetic field will be

\begin{equation*} B = \sqrt{B_x^2 + B_z^2}, \end{equation*}

and the direction will be in the \(xz\)-plane, given by the angle \(\tan^{-1}(B_z/B_x)\) with respect to the \(x\)-axis. Putting in the numerical values we obtain

\begin{align*} \amp B_x = \dfrac{4\pi\times 10^{-7}\:\textrm{T.m/A}\times 1500\:\textrm{A/m}}{2} = 9.42\times 10^{-4}\:\textrm{T} \\ \amp B_z = 4\pi\times 10^{-7}\:\textrm{T.m/A}\times 500\:\textrm{m}^{-1}\times 1\:\textrm{A} = 6.28\times 10^{-4}\:\textrm{T}. \end{align*}

These values give the net magnetic field at the field point to be approximately \(1.13\times 10^{-3}\, \text{T}\) at an angle \(33.6^{\circ}\) from the negative \(x\)-axis towards the positive \(z\)-axis.

Prev Top Next