Particle in a box is the simplest model of a bound particle. We imagine particle to be confined in a one-dimensional box. A particle will be trapped inside such a box if potential is infinite
\(U\) at both ends and zero inside the box as shown in
Figure 51.16. It turns out that potential at the edge has to be infinite if particle is to be permanently trapped. Otherwise, particle will “tunnel” through a finite barrier using a mechanism called
quantum tunneling.
First thing to note is that since potential is infinite outside the box, wavefunction for the particle will be zero putside the box.
\begin{align}
\amp \psi(x) = 0 \ \ \ x \lt 0\tag{51.15}\\
\amp \psi(x) = 0 \ \ \ x \gt 0.\tag{51.16}
\end{align}
Inside the box, wave function for energy \(E\) will satsisfy
\begin{equation}
\dfrac{d^2 \psi}{d x^2} = -\dfrac{2mE}{\hbar^2} \: \psi,\ \ \ 0 \le x \le a.\tag{51.17}
\end{equation}
Both standing wave and progressive waves are possible inside the box. Here, we solve for standing waves corresponding to specific values of energy
\(E\text{.}\) These solutions are also called
stationary states. They have angular frequency
\(\omega = E/\hbar\) and wavenumber
\(k=\sqrt{2mE}/\hbar\text{.}\) It is better to write Eq.
(51.17) as
\begin{equation}
\dfrac{d^2 \psi}{d x^2} = -k^2 \psi, \tag{51.18}
\end{equation}
where \(k\) is the wavenumber of the wave related to energy by
\begin{equation}
k^2 = \dfrac{2mE}{\hbar^2}.\tag{51.19}
\end{equation}
We seek a solution of this equation with zero value at the boundaries \(x = 0\) and \(x = a\text{.}\) IT is easy to verify that the solution will be a sine function of \(kx\) with some restrictions on \(k\text{.}\)
\begin{equation}
\psi(x) = A \sin(k x)\ \ \text{with}\ \ \psi(0) = 0 = \psi(a).\tag{51.20}
\end{equation}
It automatically satisfies \(\psi(0) = 0\text{.}\) To satisfy \(\psi(a) = 0\text{,}\) we demand
\begin{equation*}
A \sin(k a) = 0.
\end{equation*}
Since \(A \ne 0\text{,}\) we must have
\begin{equation}
k a = n \pi,\quad n = 0, \pm 1 , \pm 2, 3, \cdots. \tag{51.21}
\end{equation}
Now, if
\(n=0\) we will have
\(k=0\text{,}\) which would give
\(\psi(x) = 0\text{.}\) That would mean the particle is not even in the box. Therefore,
\(n \ne 0\text{.}\) Additionally, from Eq.
(51.19) energy
\(E\) is related to
\(k^2\text{,}\) therefore, both plus and minus values of
\(k\) correspond to the same energy. Therefore, we will drop the negative integers. Labeling the allowed values of
\(k\) by an integer index
\(n\text{,}\) the allowed values of
\(k\) will be
\begin{equation}
k_n = \dfrac{n \pi}{a},\quad n = 1 , 2, 3, \cdots.\tag{51.22}
\end{equation}
Putting these values of
\(k_n\) in Eq.
(51.19) we obtain the allowed values of energy, which will be labeled similarly with an index,
\(E_n\) to be:
\begin{equation*}
k_n = \dfrac{\sqrt{2mE_n}}{\hbar}\quad\longrightarrow\quad E_n = \dfrac{\hbar^2 k_n^2}{2m}.
\end{equation*}
That is,
\begin{equation}
E_n = \dfrac{n^2 \pi^2\hbar^2 }{2ma^2},\quad n = 1 , 2, 3, \cdots.\tag{51.23}
\end{equation}
We can write this more compactly as
\begin{equation}
E_n = n^2 E_1,\quad n = 1 , 2, 3, \cdots, \tag{51.24}
\end{equation}
with
\begin{equation*}
E_1 = \dfrac{\pi^2\hbar^2 }{2ma^2} = \dfrac{h^2 }{8ma^2}.
\end{equation*}
The wave function \(\psi\) is also labeled by the same index \(n\text{:}\)
\begin{equation}
\psi_n(x) = A\sin(k_n x) = A \sin\left( \dfrac{n \pi x}{a}\right).\tag{51.25}
\end{equation}
The constant \(A\) can be fixed by the normalization condition, which states that the probability of detecting the particle anywhere be \(1\text{.}\) Since the wave function is zero outside the box, we will have the following integral relation.
\begin{equation}
\int_{0}^{a} \psi_n^* \psi_n dx = 1.\tag{51.26}
\end{equation}
Therefore,
\begin{equation*}
\int_{0}^{a} A^2 \sin^2\left( \dfrac{n \pi x}{a}\right) dx = 1.
\end{equation*}
Taking \(A^2\) outside the integral, writing the square of the sine function in terms of the double angle of cosine, and then performing the integral immediately gives
\begin{equation*}
A^2 = \dfrac{2}{a}.
\end{equation*}
Therefore, we will have \(A = \pm\sqrt{2/a}\text{.}\) Since wave function is always used as square we drop the minus sign and use only the positive \(A\) here. This gives us the normalized wave function.
\begin{equation}
\psi_n(x) = \sqrt{\dfrac{2}{a}}\:\sin\left( \dfrac{n \pi x}{a}\right).\tag{51.27}
\end{equation}
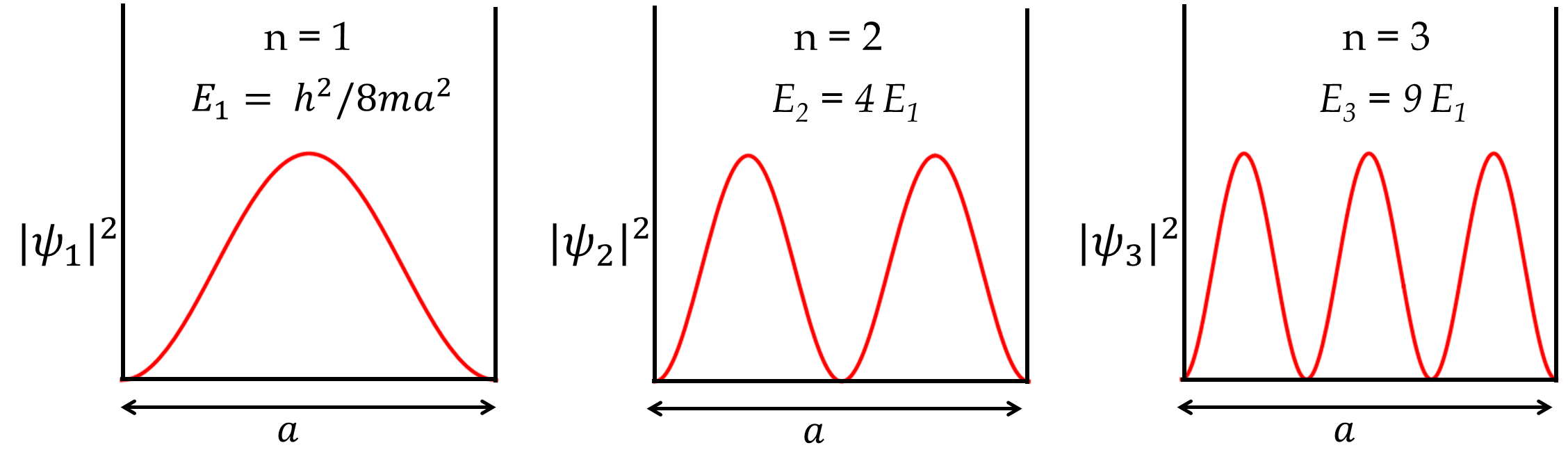
Figure 51.17 shows the probability densities corresponding to the three lowest energy states of a particle in a box.
An important point of the energy levels of the particle in a box is the separation between the states varies as \(n^2\) of the states. Thus, the separation of the energy levels \(n = n_1\) and \(n=n_2\) will be
\begin{equation}
E_{n_2} - E_{n_1} = \left( n_2^2 - n_1^2\right) E_1.\tag{51.28}
\end{equation}