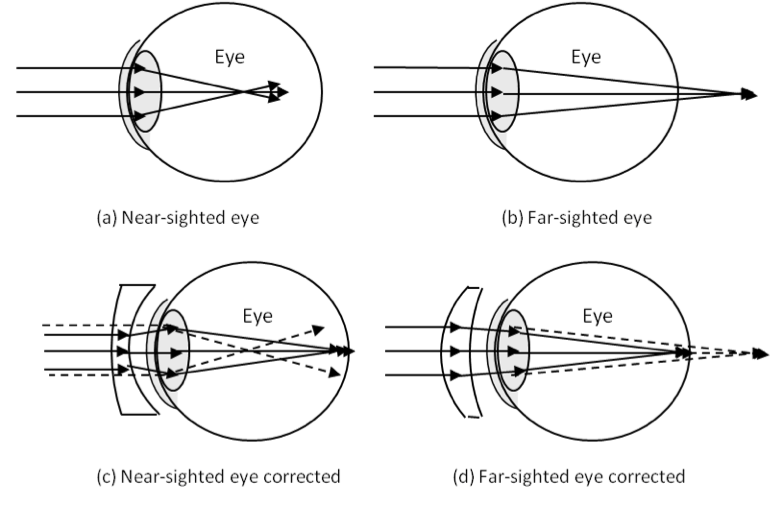
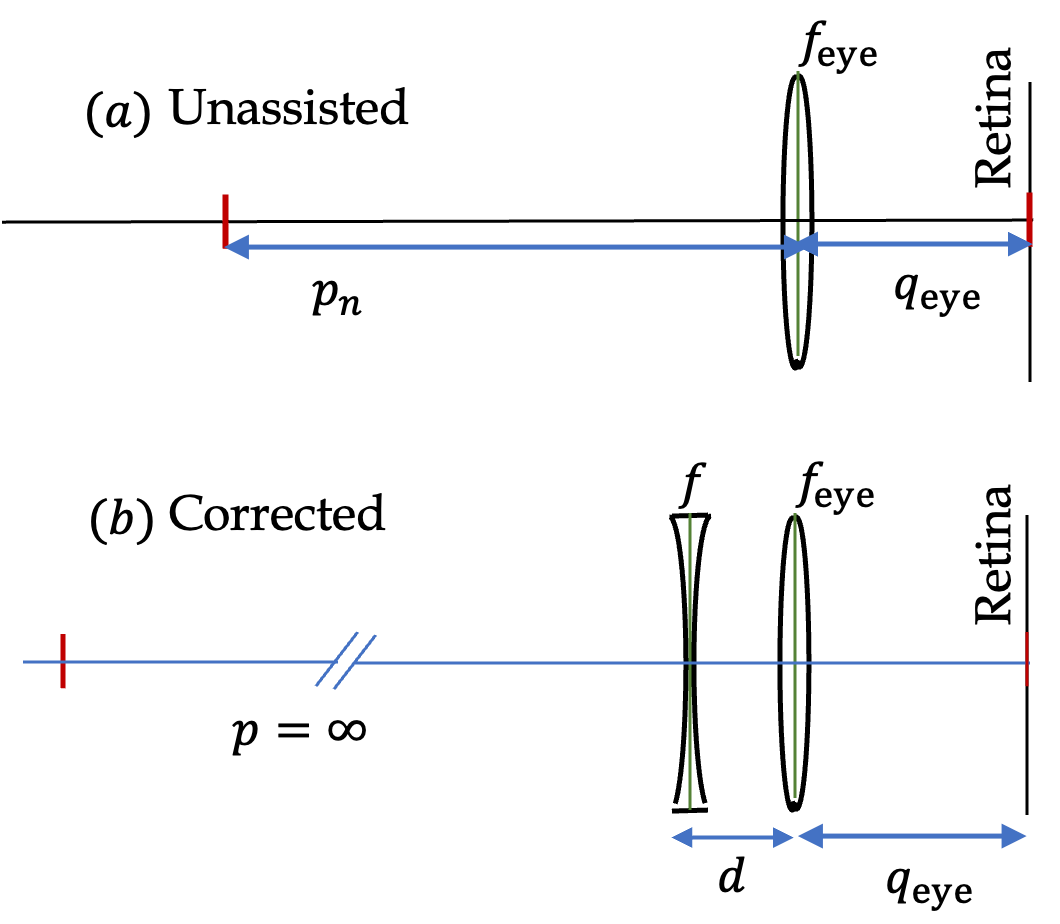
Here we have two physical situations, one without the corrective lens and the other with a diverging corrective lens. The common aspect of the two situations is the image distance of the image formed by the eye. We will generate equations in the two situations and equate \(q_\text{eye}\) from both. That should give us the condition for detemining the focal length of the corrective lens.
Figure 45.12 shows the two situations. Working with the (a), we arrive at
\begin{equation}
\frac{1}{q_\text{eye}} = \frac{1}{f_\text{eye}} + \frac{1}{p_n}, \tag{45.6}
\end{equation}
where \(p_n=52\text{ cm}\text{,}\) the near point given in the problem statement. There are two unknowns here \(q_\text{eye}\) and \(f_\text{eye} \text{.}\) We will set up second equation from the second situation.
Now, we work with (b) of the figure. Here, a point at infinity is to be focussed on the retina. Let us use symbol \(f\) for the focal length of the corrective lens, which we seek here. Note that this will be negative. First, the corrective lens, will have image at its first focal point since
\begin{equation}
\frac{1}{\infty} + \frac{1}{q} = \frac{1}{f}\ \ \rightarrow\ \ q = f.\tag{45.7}
\end{equation}
This image will be object for eye with the image length \(q_\text{eye}\text{.}\) The object distance for eye will be absolute value of \(q\) and the separation \(d\text{.}\) Therefore, we will have
\begin{equation*}
\frac{1}{|q| + d} + \frac{1}{q_\text{eye}} = \frac{1}{f_\text{eye}}.
\end{equation*}
Using Eq.
(45.6), we can get rid of both
\(q_\text{eye}\) and
\(f_\text{eye}\text{.}\) Then, using
\(q=f\) from Eq.
(45.7), we get
\begin{equation*}
\frac{1}{|f| + d} = \frac{1}{p_n}.
\end{equation*}
Therefore,
\begin{equation*}
|f| = p_n - d = 52-2 = 50\text{ cm}.
\end{equation*}
Since it is diverging lens, we have
\begin{equation*}
f = -50\text{ cm} = -0.50\text{ m}.
\end{equation*}
Therefore, the power of the lens needed is
\begin{equation*}
P = \frac{1}{f} = -2.0\text{ D}.
\end{equation*}
Another Way: With glasses on, we want an object at \(p=\infty\) to form a virtual image at the far point from the eye, which will be \(52-2=50\text{ cm}\) from the lens. Since it is a virtual image
\begin{equation*}
q_\text{lens} = -50\text{ cm}.
\end{equation*}
With \(p=\infty\text{,}\) this means
\begin{equation*}
f_\text{lens} = -50\text{ cm}.
\end{equation*}
Therefore, power of the lens
\begin{equation*}
P_\text{lens} = -2.0\text{ D}.
\end{equation*}