Section 48.8 Diffraction of Light Bootcamp
Exercises Exercises
Double-slit Diffraction
6. Interference Maxima Within Central Peak of a Double-slit Diffraction.
Follow the link : Example 48.18.7. Combined Diffraction and Interference in a Double-Slit Diffraction.
Follow the link : Example 48.19.8. Separation of Slits from Number of Interference Peaks within Central Maximum.
Follow the link : Example 48.20.Diffraction by a Circular Aperture
9. Radius of Central Bright Disk in Diffraction through a Lens.
Follow the link : Example 48.25.10. Applying Raleigh Criterion on Diffraction-limited Image from a Circular Lens.
Follow the link : Example 48.26.11. Effect of Diffraction on Resolution of an Image of Moon in Yerkes Observatory.
Follow the link : Example 48.27.12. Distance Two Objects can be Moved and Still Resolvable by Eye If Diffraction-Limited.
Follow the link : Example 48.29.Diffraction Grating
13. Wavelength from Direction of First-order Peak in a Diffraction Grating.
Follow the link : Exercise 48.7.5.1.14. Spacing Between Slits in a Diffraction Grating from the Direction of First Order Peaks.
Follow the link : Exercise 48.7.5.2.15. Number of Lines in a Transmission Diffraction Grating from Angle of Second Principal Maximum.
Follow the link : Exercise 48.7.5.3.16. Separation of Light of Different Wavelengths By a Diffraction Grating.
Follow the link : Exercise 48.7.5.4.17. Resolving the Sodium Doublet By Diffraction Grating.
Follow the link : Exercise 48.7.5.5.18. Determine if a Diffraction Grating can Resolve Mercury Yellow-Orange Doublet.
Follow the link : Exercise 48.7.5.6.19. Resolving Mercury Doublet by a Powerful Diffraction Grating.
Follow the link : Exercise 48.7.5.7.20. Resolving Power and Dispersion of a Transmission Grating.
Follow the link : Exercise 48.7.5.8.21. Resolving the Sodium Doublet.
Follow the link : Example 48.33.Miscellaneous
22. Wavelength from Diffraction Overlaps of Two Wavelengths.
A single slit is illuminated by two light waves of wavelengths 440 nm and an unknown \(\lambda\) such that the second diffraction minimum of 440-nm coincides with the third diffraction minimum for \(\lambda\text{.}\) Find \(\lambda\text{.}\)Hint.
Equate the sines of the angles of the two conditions.
Answer.
\(293.3\:\textrm{nm}\text{.}\)
Solution.
Equating the angles is the same as equating the sines of those angles. Therefore, we will get the following condition from the given data.
\begin{equation*}
\dfrac{2\times 440\: \textrm{nm}}{a} = \dfrac{3\:\lambda}{a},\ \ \Longrightarrow\ \ \lambda = 293.3\:\textrm{nm}.
\end{equation*}
23. General Formula for Number of Interference Peaks in Central Maximum of Diffraction.
Prove that in a double-slit experiment if the width \(b\) and the center-to-center distance \(a\) are related by \(a = p b\text{,}\) then the number of peaks inside the central maximum of the diffraction peak is \(2p+1\text{.}\)Hint.
First find half width or \(m^\prime=1\) minimum of the central peak of diffraction, and, then find the maximum interference order for that angle.
Answer.
\(2p+1\text{.}\)
Solution.
The half width of the central peak of the diffraction pattern gives
\begin{equation*}
b\:\sin\theta_{\textrm{hw}} = \lambda. \ \ \ \ (1)
\end{equation*}
Within this angle the maximum constructive interference order will be
\begin{equation*}
m_{\textrm{max}}\: \lambda = a\:\sin\theta_{\textrm{hw}}.\ \ \ \ (2)
\end{equation*}
The total number of constructive interference max will be
\begin{equation*}
n = 2 m_{\textrm{max}} + 1\ (\textrm{including } m = 0) = 2 p + 1\ \ (\textrm{using (1) and (2).})
\end{equation*}
24. Angular Width of Central Peak when Instrument Immersed in Water.
Red light (wavelength \(632.8\, \text{nm}\) in air) from a helium-neon laser is incident on a single slit of width \(0.05\, \text{mm}\text{.}\) The entire apparatus is immersed in water of refractive index \(\frac{4}{3}\text{.}\) Determine the angular width of the central peak.
Hint.
Wavelength wil lbe different in water.
Answer.
\(0.19\:\textrm{rad}\text{.}\)
Solution.
The wavelength in water, \(\lambda = \lambda_0/n = 474.6\,\text{nm}\text{.}\) The angular width will be obtained from twice the angle for \(m=1\) diffraction minimum.
\begin{align*}
\Delta \theta \amp = 2\theta_1\\
\amp = 2\:\sin^{-1}\left(\dfrac{\lambda}{b} \right)=2\:\sin^{-1}\left(\dfrac{ 474.6\:\textrm{nm}}{0.05\: \textrm{mm}} \right)\\
\amp = 0.19\:\textrm{rad}.
\end{align*}
25. Widening of the Central Spot of a Laser Light with Increasing Distance.
A light ray of wavelength \(461.9\, \text{nm}\) emerges from a \(2\, \text{mm}\) circular aperture of a krypton ion laser. Due to diffraction the beam expands as it moves out. How large is the central bright spot at (a) \(1\, \text{m}\text{,}\) (b) \(1\, \text{km}\text{,}\) (c) \(1000\, \text{km}\text{,}\) and (d) at the surface of the Moon at a distance of \(400,000\, \text{km}\) from the Earth.
Hint.
Find angular width in radians first, then multiply it by distance.
Answer.
(a) \(0.28\: \textrm{mm}\text{,}\) (b) \(280\: \textrm{mm}\text{,}\) (c) \(280\: \textrm{m}\text{,}\) (d) \(112\: \textrm{km}\text{.}\)
Solution.
We start with the angular width calculation.
\begin{equation*}
\Delta \theta = 1.22 \dfrac{\lambda}{D} = 1.22\: \dfrac{ 461.9\:\textrm{nm}}{2\: \textrm{mm}} = 0.00028\:\textrm{rad}.
\end{equation*}
Using \(L\Delta \theta\) we find the diameter of the beam at different \(L\)’s.
\begin{align*}
\amp \textrm{(a)}\ \ 0.28\: \textrm{mm},\\
\amp \textrm{(b)}\ \ 280\: \textrm{mm},\\
\amp \textrm{(c)}\ \ 280\: \textrm{m},\\
\amp \textrm{(d)}\ \ 112\: \textrm{km}.
\end{align*}
26. Aperture Diameter of the Telescope of a Spy Satellite.
A spy satellite is reputed to be able to resolve objects \(10\, \text{cm}\) apart while operating \(200\, \text{km}\) above the surface of the Earth. What is the diameter of the aperture of the telescope if the resolution is only limited by the diffraction effects? Use 550 nm for light.
Hint.
At the Raleigh criterion, angle of separation will equal width of the Airy’s disk.
Answer.
\(1.34\text{ m}\text{.}\)
Solution.
We can use the same setup as we used for resolving objects on the moon.
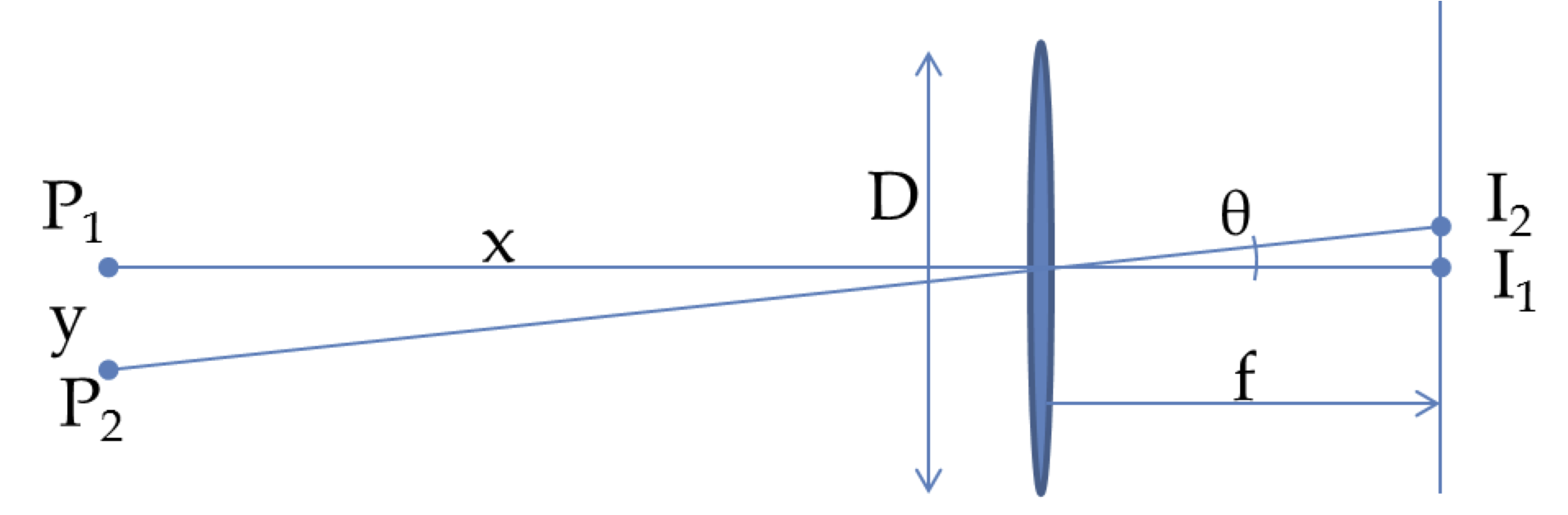
Here, we want the angular separation, \(\theta\approx y/x \) to be greater than the angular width of the Airy’s disk, namely, \(\theta_R=1.22\lambda/D\text{.}\) Therefore, we get at-the-Raleigh-criterion to be
\begin{equation*}
\frac{y}{x} = 1.22\frac{\lambda}{D}.
\end{equation*}
Therefore,
\begin{equation*}
D = 1.22\frac{ x \lambda}{y} = 1.22\frac{ 200\times 10^3 \times 550\times 10^{-9}}{0.1} = 1.34\text{ m}.
\end{equation*}

