Electric Potential of a Dipole

Section 33.4 Electric Potential of a Dipole

Electric field of a dipole far away from the dipole is called dipole field and the corresponding electric potential is called dipole potential.

Consider a dipole of moment \(\vec p\) as in Figure 33.12. What will be potential at a far away point P from it? We will show below that the electric potential of a dipole at a point far from the dipole, to be denoted by \(\phi_\text{dip}\) is

\begin{equation} \phi = \frac{1}{4\pi\epsilon_0}\,\frac{p\,\cos\theta}{r^2}.\tag{33.5} \end{equation}

You may recall that potential from a charge dropped as \(\frac{1}{r}\) when you moved away from the charge. The dipole potential, in contrast, drops much faster as \(\frac{1}{r^2}\text{.}\) So, in the case of a dipole, if you had \(12\text{ V}\) at \(r=1\text{ mm}\text{,}\) you would have \(0.12\text{ V}\) at a distance \(r=10\text{ mm}\) if you went in the same direction.

We find electric field by computing the gradient of potential and multiplying the result by \(-1\text{.}\) It is easier to do this calculation in spherical coordinates with the following result.

\begin{equation} \vec E_\text{dip} = -\vec \nabla \phi_\text{dip} = \frac{1}{4\pi\epsilon_0}\;\frac{p}{r^3}\;\left(2\cos\theta\,\hat u_r + \sin\theta\,\hat u_\theta \right).\tag{33.6} \end{equation}

It is often best to write this in coordinate-free form by absorbing the angle through the use of dot product.

\begin{equation} \vec E_\text{dip} = \frac{1}{4\pi\epsilon_0}\;\frac{1}{r^3}\;\left[ 3\,(\vec p\cdot\hat u_r)\, \hat u_r - \vec p \right].\tag{33.7} \end{equation}

Subsection 33.4.1 Derivation of Dipole Potential

Consider two equal and opposite charges \(\pm q\) separated by a distance \(d\) as shown in Figure 33.13. We wish to find formula for electric potential at point P which is far away from the dipole. We will define the meaning of far away as being

\begin{equation} r \gg d,\ \ \text{ or equivalently, }\ \ \frac{d}{r}\ll 1.\tag{33.8} \end{equation}

Using the superposition of potentials of each charge gives us

\begin{equation} \phi_P = \frac{q}{4\pi\epsilon_0}\left(\dfrac{1}{r_{+}} - \dfrac{1}{r_{-}} \right).\tag{33.9} \end{equation}

Now, we can use law of cosines in the upper triangle in the figure to get

\begin{align*} r_{+}^2 \amp = r^2 + (d/2)^2 - r d \cos\theta. \end{align*}

To apply the condition of far away given in (33.8), we pull \(r^2\) out and express right side as

\begin{align*} r_{+}^2 \amp = r^2 \left[ 1 - \frac{d}{r} \cos\theta + \frac{1}{4}\;\left(\frac{d}{r}\right)^2 \right] . \end{align*}

We see clearly that the terms on the right side are in powers of \(d/r\text{,}\) which is expected to be get small in the far away region. Let us write this as one symbol

\begin{equation*} \epsilon = \frac{d}{r}. \end{equation*}

We want \(1/r_{+}\) when \(\epsilon \ll 1 \text{.}\) Therefore,

\begin{align*} \dfrac{1}{r_{+}} \amp = \dfrac{1}{r} \left[ 1 - \epsilon \cos\theta + \frac{1}{4}\;\epsilon^2 \right]^{-1/2} \\ \amp = \dfrac{1}{r} \left[ 1 + \frac{1}{2} \epsilon \cos\theta - \frac{1}{8}\;\epsilon^2 +\frac{3}{8}\;\epsilon^2 \cos^2\theta +\cdots \right] \\ \amp = \dfrac{1}{r} + \dfrac{1}{2}\;\dfrac{d}{r^2}\;\cos\theta +\cdots \end{align*}

You can carry out similar steps using the lower triangle in the figure to get

\begin{equation*} \dfrac{1}{r_{-}} = \dfrac{1}{r} - \dfrac{1}{2}\;\dfrac{d}{r^2}\;\cos\theta +\cdots \end{equation*}

Using expressions for \(1/r_+\) and \(1/r_-\) in Eq. (33.9) we get

\begin{equation*} \phi_P = \frac{q}{4\pi\epsilon_0}\left( \dfrac{d}{r^2}\;\cos\theta + \cdots \right), \end{equation*}

where \(\cdots\) are terms with higher powers of \(d/r\text{.}\) We drop those terms since their importance decreases very rapidly compared to the leading term. We also write \(qd\) as \(p\) giving us the final expression for the dipole potential.

\begin{equation} \phi_\text{dip} = \frac{1}{4\pi\epsilon_0} \dfrac{p\cos\theta}{r^2}.\tag{33.10} \end{equation}

Subsection 33.4.2 (Calculus) Derivation of Dipole Electric Field

It is possible to carry out approximation scheme presented for the dipole potential - start from the exact field using the field of the two point charges and expand in powers of \(d/r\text{.}\) However, once we have the potential, it is much easier to just take its gradient to get the field.

Since potential in Eq. (33.10) is in spherical coordinates, we express gradient in spherical coordinates.

\begin{equation*} \vec \nabla = \hat u_r \frac{\partial }{\partial r} + \hat u_\theta \frac{1}{r} \frac{\partial }{\partial \theta}+ \hat u_\phi \frac{1}{r} \frac{\partial }{\partial \phi}. \end{equation*}

Here \(\phi\) is the azimuthal angle, and not the potential. Since potential has no azimuthal angle dependence, we need only the other two derivatives.

\begin{align*} \amp \frac{\partial \phi_\text{dip}}{\partial r} = \frac{1}{4\pi\epsilon_0} \dfrac{p\cos\theta}{r^3}\; (-2). \\ \amp \frac{\partial \phi_\text{dip}}{\partial \theta} = \frac{1}{4\pi\epsilon_0} \dfrac{p\sin\theta}{r^2}\; (-1). \end{align*}

Therefore, dipole field will be

\begin{equation*} \vec E_\text{dip} = -\vec \nabla \phi_\text{dip} = \frac{1}{4\pi\epsilon_0}\;\frac{p}{r^3}\;\left(2\cos\theta\,\hat u_r + \sin\theta\,\hat u_\theta \right). \end{equation*}

Example 33.14. Force Between an Electric Dipole and a Point Charge.

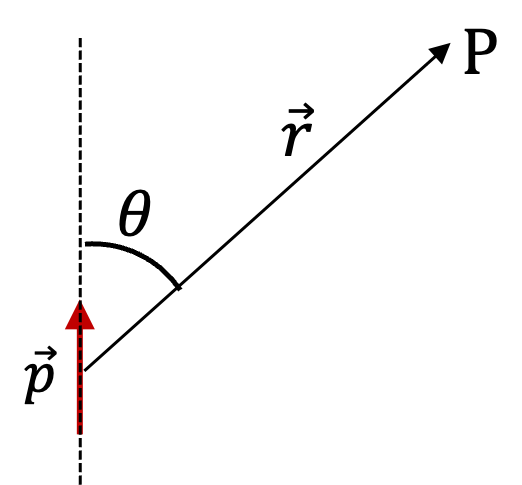
A point charge \(Q\) is at a distance \(D\) from a dipole of dipole monent \(p\text{.}\) The displacement vector of the charge \(Q\) makes an angle \(\theta\) with respect to the direction of the dipole moment vector \(\vec p\text{.}\) (a) Find the electric force on \(Q\text{.}\) (b) Find the electric potential energy of \(Q\text{.}\)

Answer.

(a) \(\frac{1}{4\pi\epsilon_0}\;\frac{Qp}{D^3}\;\left(2\cos\theta\,\hat u_r + \sin\theta\,\hat u_\theta \right)\text{,}\) (b) \(\frac{1}{4\pi\epsilon_0} \dfrac{Qp\cos\theta}{D^2}\text{.}\)

Solution.

(a) The force on \(Q\) will be the product of \(Q\) and electric field at \(Q\text{.}\) The electric field at \(Q\) is by the dipole. Therefore, the force on \(Q\) will be

\begin{equation*} \vec F_{\text{on }Q} = \frac{1}{4\pi\epsilon_0}\;\frac{Qp}{D^3}\;\left(2\cos\theta\,\hat u_r + \sin\theta\,\hat u_\theta \right). \end{equation*}

(b) The potential energy of \(Q\) will be product of \(Q\) and potential at \(Q\) by the dipole. Therefore,

\begin{equation*} U_{\text{of }Q} = \frac{1}{4\pi\epsilon_0} \dfrac{Qp\cos\theta}{D^2}. \end{equation*}

Example 33.15. Force on a Point Charge from an Electric Dipole.

A tiny electric dipole of moment \(5.0\times 10^{-15}\text{ Cm}\) is located at the origin and points in the positive \(z\) axis direction. Suppose this dipole is fixed there.

A particle of charge \(-4.0\times 10^{-15}\text{ C}\) and mass \(2.0\times 10^{-18}\text{ kg}\) is released from rest on the positive \(z\) axis at \(z=3.0\text{ mm}\text{.}\)

(a) What is the force on the charge immediately after it is released?

(b) The negativel partile is seen to move towards the dipole. What is the speed of the particle when it reaches \(z=1\text{ mm}\text{?}\)

Answer.

(a) \(-1.33\times 10^{-11}\text{ N}\ \hat u_z\text{,}\) (b) \(400\text{ m/s}\text{.}\)

Solution 1. (a)

The electric field by the dipole at the location of the particle will be given by setting \(\theta=0\) in the formula given above.

\begin{align*} \vec E_\text{dip} \amp = \frac{1}{4\pi\epsilon_0}\;\frac{p}{r^3}\;\left(2\cos\theta\,\hat u_r + \sin\theta\,\hat u_\theta \right)\\ \amp = \frac{1}{2\pi\epsilon_0}\;\frac{p}{z^3}\;\hat u_z = \frac{10^4}{3}\text{ N/C}\ \hat u_z. \end{align*}

Therefore, force will be

\begin{align*} \vec F \amp = -4.0\times 10^{-15}\text{ C} \times \frac{10^4}{3}\text{ N/C}\ \hat u_z \\ \amp = -1.33\times 10^{-11}\text{ N}\ \hat u_z. \end{align*}

Solution 2. (b)

Note that acceleration is not constant, so we cannot use constant acceleration formulas here. But, if we use conservation of energy, we can get speed we seek. With zero kinetic energy at the start, we get

\begin{equation*} Q\phi_\text{start} = \frac{1}{2}mv^2 + Q\phi_\text{end}. \end{equation*}

Therefore, we get

\begin{align*} v^2 \amp = \frac{2Q}{m} \left( \phi_\text{start} - \phi_\text{end} \right)\\ \amp =\frac{p}{4\pi\epsilon_0} \frac{2Q}{m} \left( \frac{1}{z_1^2} - \frac{1}{z_2^2} \right) \\ \amp = 9\times 10^9 \times 5.0\times 10^{-15} \times \frac{2 \times -4.0\times 10^{-15}}{2.0\times 10^{-18}}\times\\ \amp\ \ \ \ \ \ \ \ \ \ \left( \frac{1}{0.003^2} - \frac{1}{0.001^2} \right) \\ \amp = 160,000\text{ m}^2/\text{s}^2. \end{align*}

This gives \(v = 400\text{ m/s}.\)

Example 33.16. Torque on a Dipole from Field of another Electric Dipole.

Figure 33.17 shows two dipoles. (a) Find the torque on dipole \(p_2\text{.}\) (b) Find the torque on dipole \(p_1\text{.}\)

Answer.

(a) \(\frac{1}{4\pi\epsilon_0}\, \frac{p_1 p_2\sin\theta}{a^3}\,\hat u_y\text{,}\) (b) \(\frac{1}{4\pi\epsilon_0}\, \frac{2p_1 p_2\sin\theta}{a^3}\,\hat u_y\text{.}\)

Solution 1. (a)

The torque on \(p_2\) will be \(\vec\tau = \vec p_2 \times \vec E_1\text{,}\) where \(\vec E_1\) is the electric field of \(p_1\) at the location of \(p_2\text{.}\)

Using the coordinates in Figure 33.18, the electric field of \(\vec p_1=p_1 \hat u_z\) at location of \(p_2\) at \(x=a,y=0,z=0\) will be

\begin{equation*} \vec E_1 = -\frac{1}{4\pi\epsilon_0}\, \frac{p_1}{a^3}\,\hat u_z. \end{equation*}

You can easily get this answer in you set \(\hat u_r=\hat u_x\) in Eq. (33.7). Since \(\hat p_2 = p_2\sin\theta\, \hat u_x + p_2\cos\theta\, \hat u_z\text{,}\) for torque on \(p_2\) we get

\begin{equation*} \vec \tau_2 = \frac{1}{4\pi\epsilon_0}\, \frac{p_1 p_2\sin\theta}{a^3}\,\hat u_y. \end{equation*}

This will cause angular acceleration of the dipole about positive \(y\) axis.

Solution 2. (b)

We use the same figure as in (a). To get the electric field of \(\vec p_2\text{,}\) we note that \(r=a\text{,}\) same as (a), but now \(\vec p_2 = -p_2\,\sin\theta\,\hat u_x + p_2\,\cos\theta\, \hat u_z\text{.}\) Using this in the coordinate-free form of electric field, given in Eq. (33.7), we obtain electric field of \(p_2\) at the location of \(p_1\text{.}\)

\begin{align*} \vec E_2 \amp = \frac{1}{4\pi\epsilon_0}\; \frac{1}{a^3} \left( [\vec p_2\cdot (-\hat u_x)]\,(-\hat u_x) - \vec p_2\right)\\ \amp = \frac{1}{4\pi\epsilon_0}\; \frac{1}{a^3} \left( 2\sin\theta\,\hat u_x - \cos\theta\,\hat u_z \right). \end{align*}

Now, with \(\vec p_1 = p_1\hat u_z\text{,}\) we get the torque \(\vec p_1\times \vec E_2\) to be

\begin{equation*} \vec \tau_1 = \frac{1}{4\pi\epsilon_0}\, \frac{2p_1 p_2\sin\theta}{a^3}\,\hat u_y. \end{equation*}

Prev Top Next