Impulse

Section 7.2 Impulse

Definition of Impulse.

When you hit a baseball, you change direction and magnitue of the momentum of the ball in a very short duration of time. The change in momentum is caused by the force from the bat acting on the ball during the time they were in contact with each other.

If you look at the magnitude of the force on the ball, it will be initially zero till contact occurs, will increase as the bat crushes into the ball, and then, will decrease to zero as the ball leaves the bat. The stronger the force and/or the longer the force acts on the ball, the greater the change in the momentum of the ball.

That is, both the magnitude of the force and the time are important for causing a change in momentum. For this purpose, we define impulse, \(\vec J\text{,}\) during an infintesimal interval \(\Delta t\) by product of the force \(\vec F\) and the interval.

\begin{equation} \vec J = \vec F \;\Delta t.\tag{7.4} \end{equation}

For constant force \(\vec F_0\text{,}\) such as weight, impulse over a finite interval \(t_1\le t \le t_2\) will be

\begin{equation} \vec J = \vec F_0 \;(t_2 - t_1).\tag{7.5} \end{equation}

If force is changing with time, as for example the force shown in Figure 7.13, we will need to integrate \(\vec F(t)\) with respect to time \(t\text{,}\) or, work with area under the curve of the components of force versus time. Thus, impulse is formally defined by the following “conceptual integral”

\begin{equation} \vec J = \int_{t_1}^{t_2}\vec F(t) \;dt\ \ \ (\text{Calculus/Formal Defintion}).\tag{7.6} \end{equation}

The Cartesian components of impulse will be integrals that you can perform from given funtions \(F_x(t)\text{,}\) \(F_y(t)\text{,}\) \(F_z(t)\text{.}\)

\begin{equation} J_i = \int_{t_1}^{t_2}\vec F_i(t) \;dt\ \ \ (i = x, y, z).\tag{7.7} \end{equation}

Previously, we have seen that another way to look at integrals is “area under the curve”. Thus, \(J_x\) during interval \(t_1\le t \le t_2\) will be area between \(F_x(t)\) and \(F_x=0\) when you plot \(F_x\) versus \(t\text{.}\)

\begin{equation} J_i = \text{area under }F_i \text{ vs }t\text{ plot.}\ \ \ (i=x,y,z) \tag{7.8} \end{equation}

From the components \((J_x, J_y, J_z)\text{,}\) we can obtain the mangitude and direction of impulse as we do for any other vector quantity.

Subsection 7.2.1 Impulse as Area under/over Force Components

Often the data for force with respect to time is in terms of a plot of force versus time as shown in Figure 7.12. If you can write the data as an analytic function of time using a coordinate system for direction of the force, you will have three plots, \(F_x \text{ vs } t\text{,}\) \(F_y \text{ vs } t\text{,}\) and \(F_z \text{ vs } t\text{.}\) From these you can obtan the cartesian components of the impulse vector.

Alternately, we can utilize another interpretation of the definite integral of one variable: a definite integral of a function \(f(t)\) of one independent variable \(t\) is equal to the area under the curve of \(f(t)\) versus \(t\) plot. The area for a curve above the abscissa gives a positive area and the area for a curve below the abscissa has a negative area. The integral value for integration from \(t=t_1\) to \(t=t_2\) is the sum of all areas under the curve between the limits, \(t_1\le t\le t_2\text{.}\)

Let us look at one of the Cartesian components, say the \(x\)-component. A plot of \(x\)-component of a force is shown in Fig. \ref{fig:area-under-curve-1}.

Figure 7.14. Area under curve shown shaded is evaluated from the sum of the areas of rectangles of the area. In the limit of infinitesimal \(t\) subintervals the area obtained from summing the areas of the rectangles approaches the exact area under the curve.

The shaded part has an “area under the curve” of \(F_x(t_i)\Delta t\text{,}\) which is the contribution to the \(x\)-component of the impulse for the time segment \(t_i\) to \(t_{i+1}\) of duration \(\Delta t\text{.}\) You can easily see that the area \(F_x(t_i)\Delta t\) is not really equal to the ``true’’ area under the curve - the rectangle misses the curve by some amount depending upon the size of \(\Delta t\) and how curved the curve is at that point in the plot. However, as you make \(\Delta t\) progressively smaller, the difference between the exact area and the approximate area evaluated by rectangles becomes progressively smaller, and the two become more and more equal to each other. By choosing small enough \(\Delta t\) we can make the error less than any desired value.

To obtain an exact value of the integral of \(F_x\) from \(t=0\) to \(t=T\) from a plot of \(F_x\) versus \(t\text{,}\) we divide the total interval, \(0\le t\le T\text{,}\) into subintervals of size \(\Delta t\text{,}\) and sum over the areas of the rectangles. If \(\Delta t\) is small enough, then the value obtained by summing the areas gives us the exact value of the integral.

\begin{align} \int_0^T F_x dt \amp = \lim_{\Delta t\rightarrow 0} \left[ F_x(0)\Delta t + F_x(\Delta t)\Delta t + F_x(2\Delta t)\Delta t + \cdots \right] \tag{7.9}\\ \amp = \textrm{Area under}\, F_x \text{ vs } t \text{ from } t=0 \text{ to } t=T.\tag{7.10} \end{align}

The same procedure will work for the \(y\) and \(z\)-components also. The “area under the curve” method provides an alternate way of evaluating components of impulse vector.

\begin{align} \amp J_{net,x} = \int_0^T F_x(t) dt = \text{Area under}\ F_x \text{ vs } t.\tag{7.11}\\ \amp J_{net,y} = \int_0^T F_y(t) dt = \text{Area under}\ F_y \text{ vs } t.\tag{7.12}\\ \amp J_{net,z} = \int_0^T F_z(t) dt = \text{Area under}\ F_z \text{ vs } t.\tag{7.13} \end{align}

Example 7.15. Impulse from the Area under \(F \) versus \(t \).

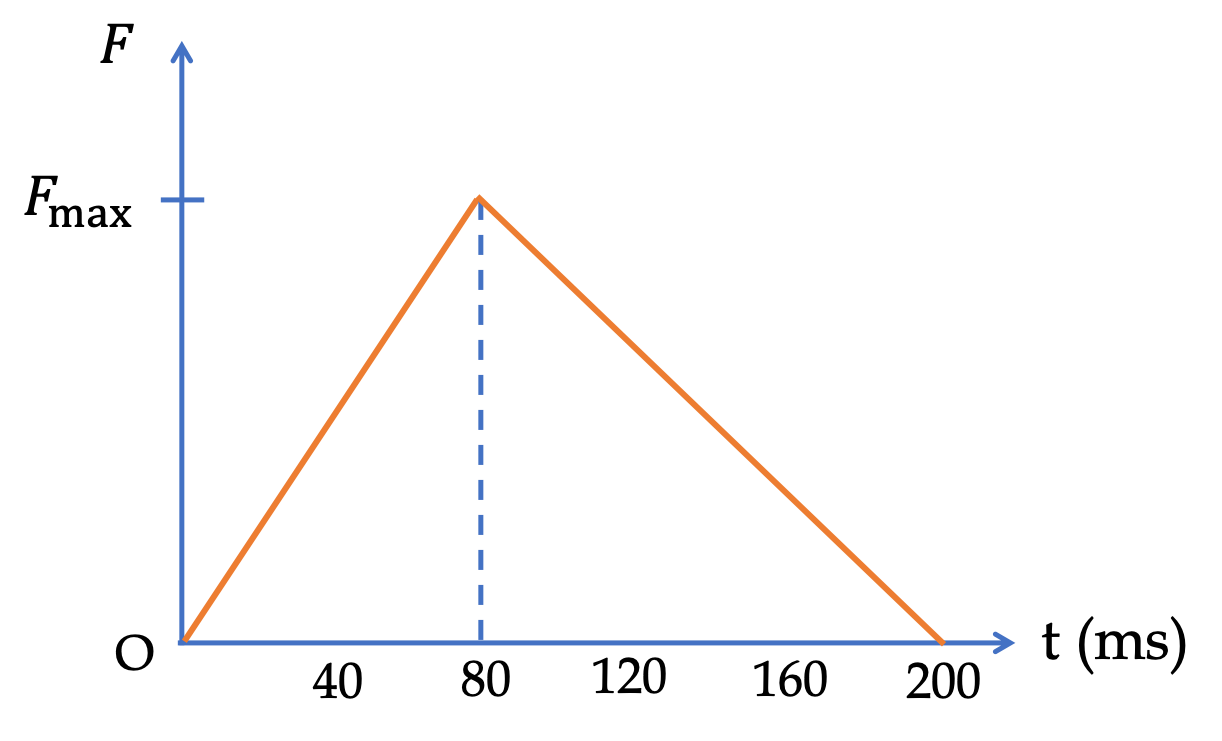
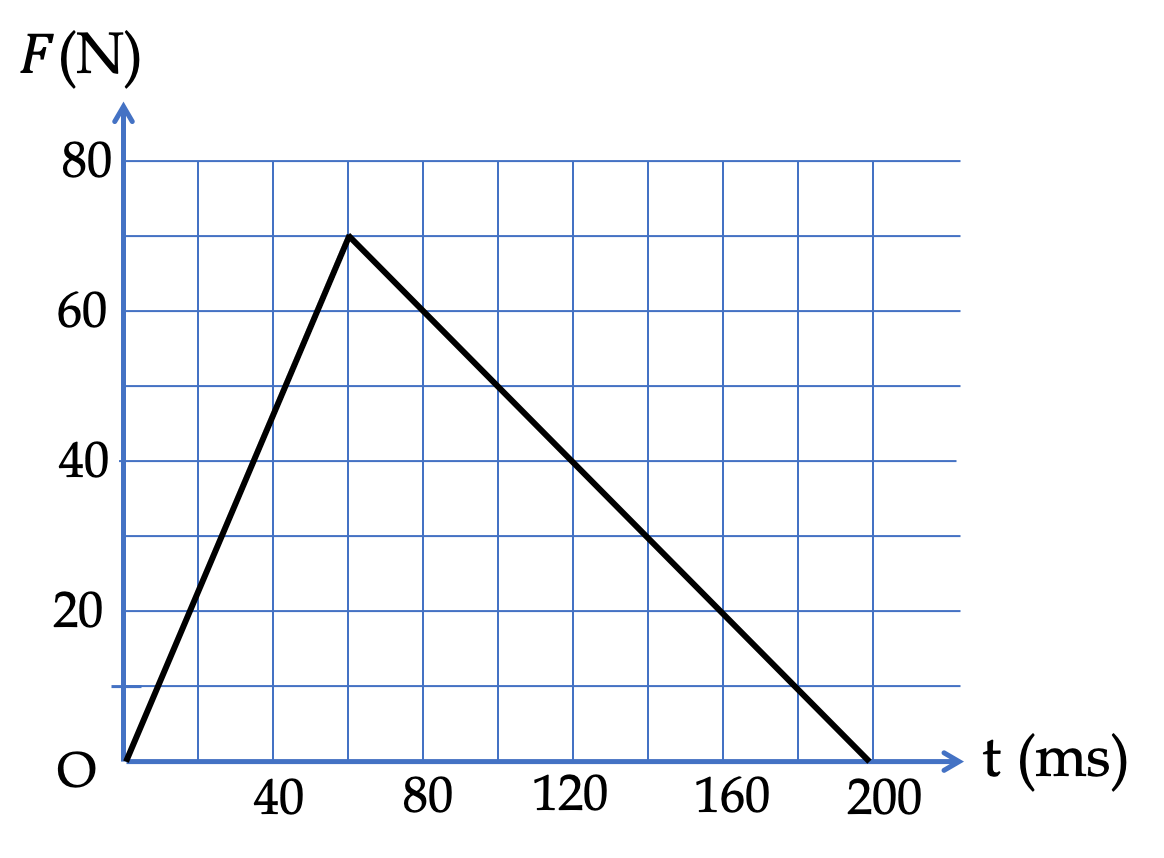
The impulse of a baseball hit can be well-approximated by a hat-shaped curve as shown in Figure 7.16. The direction of the force during the hit is nearly constant, in the direction from the bat towards the ball. From the given values on the graph find the magnitude of the impulse on the ball.

Answer.

\(7.0\text{ N.s}.\)

Solution.

Since direction of the force does not change, we can take that direction to be direction of positive \(x\) axis. In this case, \(J_y=J_z=0\text{,}\) and magnitude \(J = J_x\text{.}\)

Therefore, we can compute the magnitude of impulse from the area under the curve of magnitude \(F\) versus \(t\text{.}\) The area is area of triangle, whose formula is

\begin{equation*} A = \dfrac{1}{2}\times \text{ base }\times \text{height}. \end{equation*}

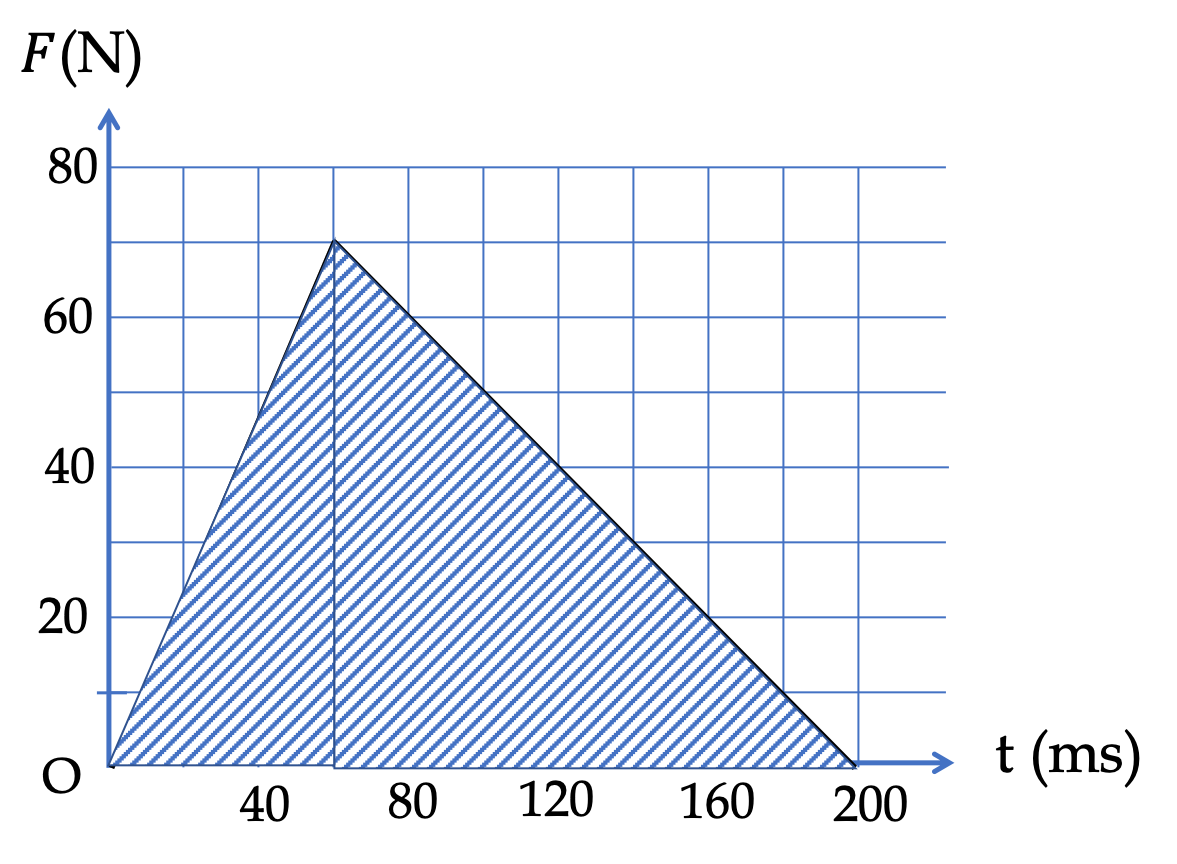
We also notice that the unit of time is in milli-sec, which we will express in seconds. Therefore, we get

\begin{equation*} J = \dfrac{1}{2}\times 70\text{ N}\times 200\times 10^{-3}\text{ s} = 7.0\text{ N.s}. \end{equation*}

Subsection 7.2.2 (Calculus) Impulse as an Integral

Consider an interval \(t=t_i\) to \(t=t_f\) during which we wish to compute the impulse of a force \(\vec F \text{,}\) whose direction is fixed in time, for simplicity. Here, we will show how the formula for the magnitude of impulse is derived.

Let us divide the interval into \(N \) subintervals: \((t_0=t_i, t_1)\text{,}\) \((t_1, t_2)\text{,}\) \((t_2, t_3)\text{,}\) \(\cdots\text{,}\) \((t_{N-2}, t_{N-1})\text{,}\) and \((t_{N-1}, t_N=t_f)\text{.}\) For simplicity, let the intervals be of equal length in time, \(\Delta t\text{,}\)

\begin{equation*} \Delta t = \dfrac{t_f - t_i}{N}. \end{equation*}

Figure 7.18. The impulse of a force over an interval \((t_i, t_f) \) can be computed by dividing the interval into a large number of subintrevals, computing the magnitude of impulses for each subinterval, and then adding them up. During the subinterval \((t_{k-1}, t_{k}) \text{,}\) the magnitude of force at the ends of the interval are \(F_{k-1} \) and \(F_{k}\) respectively, whose average is denoted by \(F_{k}^{\text{av}}\text{.}\)

Now, let us compute the impulse magnitude \(J_k\) in the \(k^{\text{th}}\) subinterval. Let the magnitude of the force at the ends of this subinterval be \(F_{k-1} \) and \(F_{k} \text{.}\) If \(N \) is large enough, then \(F_{k-1} \) and \(F_{k} \) will be almost the same, and therefore, we can get a good approximation of impulse magnitude \(J_k\) by using the average force in the subinterval as

\begin{equation*} J_k \approx F_{k}^{\text{av}}\, \Delta t \end{equation*}

We now add up impulses from every subinterval to get the impulse over the original interval.

\begin{equation*} J \approx \sum_{k=1}^{N} \, F_{k}^{\text{av}}\, \Delta t. \end{equation*}

By increasing \(N \) as large as we like, we can make this aproximation as accurate as we are happy with. The limit \(N \rightarrow \infty \) is said to be the exact value, which is represented by the integral sign.

\begin{equation} J = \int_{t_i}^{t_f}\, F(t) dt.\tag{7.14} \end{equation}

If we are dealing with a force whose magnitude as well as direction changes, then we will work with one component at a time. The same procedure as above will give us the components of the impulse vector.

\begin{align} \amp J_x = \int_{t_i}^{t_f}\, F_x(t) dt,\tag{7.15}\\ \amp J_y = \int_{t_i}^{t_f}\, F_y(t) dt,\tag{7.16}\\ \amp J_z = \int_{t_i}^{t_f}\, F_z(t) dt.\tag{7.17} \end{align}

From \((J_x, J_y, J_z)\) you can compute the magnitude and direction of the impulse in a usual way.

Example 7.19. (Calculus) Impulse of a Force Varying in Time Given as a Function of Time.

A train is pulled by another train with increasing force magnitude for a total duration of \(5\text{ sec}\) with the direction of the force unchanged. The magnitude of the force is given to be \(F(t) = 60\,t^2 + 2000\) in units of \(\text{N}\text{.}\) What is the impulse magnitude?

Answer.

\(12,500\, \text{N.s}\text{.}\)

Solution.

Since direction of force is unchanging, we take that direction to be \(x\) axis. This will make magnitude \(J\) equal to \(J_x\text{.}\) That is, we can just integrate magnitude of force to obtain the answer.

\begin{align*} J \amp = J_x = \int\, F_x(t) dt = \int\, F(t) dt\\ \amp = \int_0^5 \left( 60\,t^2 + 2000 \right)\, dt \\ \amp = \left( \dfrac{1}{3}\times 60\times 5^3 + 2000\times 5 \right) = 12,500\, \text{N.s} \end{align*}

Subsection 7.2.3 Net Impulse

Impulses from different forces add vectorially. Suppose force \(\vec F_1\) acts for a time \(\Delta t_1\) and \(\vec F_2\) for a time \(\Delta t_2\text{,}\) then the net impulse \(\vec J_{\text{net}}\) will be the vector sum of the impulses \(\vec J_1\) and \(\vec J_2\) of the two forces.

\begin{equation*} \vec J_{\text{net}} = \vec J_{1} +\vec J_{2}, \end{equation*}

which must be evaluated as vector additions that you have learned in previous chapters. You can, of course, extend this to any number of forces in an obvious way.

Example 7.20. Net Impulse of Two Forces.

A box is on a level surface. A force of magnitude \(3\text{ N}\) acts on the box in the direction towards the East for \(10\text{ sec}\) and another force of magnitude \(8\text{ N}\) acts on the box in the direction towards the North for \(5\text{ sec}\text{.}\)

What are the magnitude and direction of the net impulse?

Answer.

\(50\text{ N.s}\text{,}\) \(53.1^{\circ} \) is the counterclockwise angle from the positive \(x \) axis.

Solution.

Let us work this problem out analytically. (You could just as easily do it graphically.) Let positive \(x \) axis be towards East and the positive \(y \) axis towards North. then, we find the following for the two impulse vectors.

\begin{align*} \amp J_{1x} = 3\times 10 = 30\text{ N.s},\ \ J_{1y} = 0,\\ \amp J_{2x} = 0\ \ J_{2y} = 8\times 5 = 40\text{ N.s}. \end{align*}

Adding these vectorially we get the components of the net impulse

\begin{align*} \amp J_x^{\text{net}} = J_{1x} +J_{2x} = 30 + 0 = 30\text{ N.s},\\ \amp J_y^{\text{net}} = J_{1y} +J_{2y} = 0 + 40 = 40\text{ N.s}. \end{align*}

This gives the following for the magnitude and angle with respect to the \(x \) axis.

\begin{align*} \amp J_{\text{net}} = \sqrt{30^2 + 40^2} = 50\text{ N.s},\\ \amp \theta = \tan^{-1}\left( \dfrac{40}{30}\right) = 53.1^{\circ}. \end{align*}

We use the angle value and the quadrant of \((J_x,\, J_y) \) to interpret the direction. Here, since \((30,\, 40) \) is in the first quadrant, the angle \(53.1^{\circ} \) is the counterclockwise angle from the positive \(x \) axis.

Exercises 7.2.4 Exercises

1. Find Maximum Force from Given Impulse and Force Graph.

The graph shows a hat-shaped function for the magnitude of a force as a function of time. By observing change in the momentum of the body, it was estimated that the impulse of the force is \(10.0\text{ N.s}\text{.}\) What is the value of \(F_\text{max}\text{?}\)

Hint.

Equate the area under the curve to the impulse.

Answer.

\(F_\text{max} = 100\text{ N}\text{.}\)

Solution.

First we find an expression for the impulse from area under the given graph. Then, we equate it to find an equation in the unknown \(F_\text{max}\text{.}\) We also convert the unit of time to sec from the msec given in the graph. From the graph we get

\begin{equation*} J = \dfrac{1}{2}\, 0.200\, F_\text{max} = 0.1\, F_\text{max}. \end{equation*}

Thus,

\begin{equation*} 0.1\, F_\text{max} = 10.0\text{ N.s}. \end{equation*}

This gives \(F_\text{max} = 100\text{ N}\text{.}\)

2. Impulse from Force Component Graphs in a Two-dimensional Situation.

The graph shows the \(x\) component of a force as a function of time. At \(t = 0\text{,}\) the \(x\) and \(y\) components of the momentum of the body upon which this force acts had the values \(p_x = 10\text{ kg.m/s}\) and \(p_y = -20\text{ kg.m/s}\text{.}\) Find the magnitude and direction of the momentum at \(t = 200\text{ ms}\text{.}\)

Figure 7.23. Force components versus time for Exercise 7.2.4.2.

Hint.

Work out the \(x\) and \(y\) components separately.

Answer.

\(6.32\text{ N.s}\text{,}\) \(72^{\circ} \) clockwise from negative \(x\) axis

Solution.

The area under the curves gives us the components of impulse.

\begin{align*} J_x \amp = \dfrac{1}{2}\times 100 \times 0.08 + (-50)\times 0.12 = -2\text{ N.s},\\ J_y \amp = -\dfrac{1}{2}\times 50 \times 0.04 + \dfrac{1}{2}\times 50 \times 0.04 + 50\times 0.12 = 6\text{ N.s}. \end{align*}

Therefore, the magnitude of impluse is

\begin{equation*} J = \sqrt{J_x^2 + J_y^2} = \sqrt{2^2 + 6^2} = 6.32\text{ N.s}. \end{equation*}

Angle with \(x\) axis is

\begin{equation*} \theta = \tan^{-1}\left( \frac{6}{-2}\right) = -72^\circ. \end{equation*}

Since point \((-2,6)\) is in the second quadrant, the diration is \(72^\circ\) clockwise from the negative \(x\) axis.

3. (Calculus) Impulse of a Sinusoidally Varying Force.

The time dependence of a sinusoidally varying force can be written as a sine or cosine of time. For instance, when an electron is illuminated by a monochromatic light, the force on the electron varies as a cosine or sine function or a combination thereof.

Suppose the force on an electron at some instant \(t \) has the following form with respect to a coordinate system,

\begin{equation*} \vec F = A \cos (2\pi f t)\, \hat i + B \sin(2\pi f t)\, \hat j\text{,} \end{equation*}

where \(\hat i\) and \(\hat j\) are the unit vectors along the \(x\) and \(y\) axes respectively, \(A\) and \(B\) are some constants, and \(f \) is also a constant frequency.

What will be the magnitude and direction of the impulse on the electron during an interval \(t=0 \) to \(t=T\) for the case \(A = B \text{?}\)

Hint.

Find the components \(J_x\) and \(J_y\)

Answer.

\(\dfrac{A}{\pi f}\left|\sin(\pi f T) \right| \text{,}\) direction \(\pi f T \mod 2\pi \text{.}\)

Solution.

We can find the components of the impulse vector and then write the full impulse vector using the components and the unit vectors.

\begin{align*} J_x \amp = \int_0^T\, A \cos (2\pi f t)\, dt = \dfrac{A}{2\pi f}\, \sin (2\pi f T), \\ J_y \amp = \int_0^T\, A \sin (2\pi f t)\, dt = -\dfrac{A}{2\pi f}\, \left[ \cos (2\pi f T) - 1 \right]. \end{align*}

Therefore, using unit vectors, the impulse vector is

\begin{equation*} \vec J = J_x\, \hat i + J_y\, \hat j, \end{equation*}

from which we can get the magnitude to be

\begin{align*} J \amp = \sqrt{J_x^2 + J_y^2},\\ \amp = \dfrac{A}{2\pi f} \sqrt{2-2\cos(2\pi f T)},\\ \amp = \dfrac{A}{2\pi f} \sqrt{4\sin^2(\pi f T)},\\ \amp = \dfrac{A}{\pi f}\left|\sin(\pi f T) \right|, \end{align*}

and the angle for the line

\begin{align*} \theta \amp = \tan^{-1}\left(\dfrac{J_y}{J_x} \right), \\ \amp = -\tan^{-1}\left(\dfrac{\cos(2\pi f T) - 1}{\sin(2\pi f T)} \right), \\ \amp = \tan^{-1}\left(\dfrac{2\sin^2(\pi f T)}{2\sin(\pi f T)\cos(\pi f T)} \right), \\ \amp = \tan^{-1}\left(\tan(\pi f T) \right) = \pi f T, \end{align*}

where the direction will be based on interpreting this angle \(mod\ 2\pi\text{.}\)

Prev Top Next