Translational Motion of Macroscopic Bodies

Section 7.5 Translational Motion of Macroscopic Bodies

By translational mtion of a macroscopic body we will mean the motion of the whole body regardless of its orientation of changing shape. We say that we are interested in describing the motion of the group of particles making up the macroscopic body as a whole. A baton, for instance, with two masses connected by a light rod, as a whole, moves as a two-particle system. When you throw a baton in the air, the two masses tumble about each other and move under the influence of gravity of the Earth. Although the motion of each mass is quite complicated, we are often interested in an overall motion of the baton.

Figure 7.55. A baton with two masses moves as a two-particle system. In this sectio we will find that the total momentum of the two masses is affected only by the external force on the two masses.

The physics of multipoarticle systems are based on the physics of individual particles of the system. When we apply Newton’s laws of motion to each particle we obtain the rate of change of momentum of each particle. These rules for individual particles can be combined to deduce the overall motions, such as the overall translational and the rotational motion of the multiparticle system. In this section, we will see how the total momentum of a multiparticle system can be studied. The rotational motion of multiparticle systems will be studied in a later chapter.

Subsection 7.5.1 Two-Particle System

As a an example of a multiparticle system, let us examine a two-particle system first. We take a familiar example from Astronomy and study the motion of the Earth and the Moon together as one multiparticle system. To keep the physical situation simple we will ignore other planets and consider only the Sun as the sole external object with which the Earth and the Moon can interact as shown in Figure 7.56 in addition to their interaction with each other.

Figure 7.56. In the three-body world of the Earth, the Moon and the Sun, when we wish to study the motions of the Earth and the Moon, then they form a two-particle system and the Sun becomes an external body to the system. Had we decided to study the motion of the Earth only, then the Earth would be a one-body system and the Moon and the Sun would have been the external bodies to the system. Had we decided to study the motions of all three bodies shown, then the system would be a three-body system, and since there is nothign external to this system, the system would have been an isolated system.

To simplify the notation we will use subscript $1$ for the Earth, $2$ for the Moon, and $ext$ for the Sun in our calculations below.

Let us start with the separate equations of motion of the two objects in the system as given by Newton’s second law of motion.

\begin{align} \amp \text{Earth: }\ \ \frac{d\vec p_1}{dt} = \vec F_1^{\text{ext}} + \vec F_{12}.\tag{7.41}\\ \amp \text{Moon: }\ \ \frac{d\vec p_2}{dt} = \vec F_2^{\text{ext}} + \vec F_{21}.\tag{7.42} \end{align}

where $\vec F_{12}$ is the force on the Earth by the Moon, $\vec F_1^{\text{ext}}$ is the force of the Sun on the Earth, $\vec F_{21}$ is the force on the Moon by the Earth, and $\vec F_2^{\text{ext}}$ is the force of the Sun on the Moon. Note that forces of the Moon on the Earth and that of the Earth on the Moon are internal forces for the system since the Earth and Moon belong to the multiparticle system. Only the forces by Sun on the Earth and Moon are external to the Earth-Moon system.

According to Newton’s third law, the internal forces $\vec F_{12}$ and $\vec F_{21}$ are equal in magnitude but act in opposite directions. Hence their vector sum must be zero.

\begin{equation} \vec F_{12} + \vec F_{21} =0.\tag{7.43} \end{equation}

This suggests that we should add equations (7.41) and (7.42), which will result in an equation without any reference to the internal forces.

\begin{equation} \frac{d\left(\vec p_1 +\vec p_2\right) }{dt} = \vec F_1^{ext} + \vec F_2^{ext},\tag{7.44} \end{equation}

which can be re-written more compactly as

\begin{equation} \frac{d\vec P_{\text{system}} }{dt} = \vec F_{net}^{ext}.\tag{7.45} \end{equation}

where I have written $\vec P_{\text{system}}$ for the total momentum $\vec p_1 +\vec p_2$ and $\vec F_{\text{net}}^{\text{ext}}$ for the sum of all the external forces on the Earth-Moon system. Thus, we find that the rate of change of total momentum of a composite system depends only on the external forces, and completely independent of the internal forces. Therefore, even if you do not know anything about the internal forces of a composite system, you can still predict the translational motion of the system as a whole by looking at the total momentum vector.

Subsection 7.5.2 Generalization to Multiparticle Systems

From the procedure outlined above for a two-particle system it is clear what to expect for the total momentum of an arbitrary number $N$ of particles instead of just two. The following is a summary of results one can easily obtain.

Let $\vec P_{\text{system}}$ be the total momentum of the system of $N$ particles, i.e.,

\begin{equation*} \vec P_{system} = m_1\vec v_1 + m_2\vec v_2 + \cdots + m_N\vec v_N. \end{equation*}

The rate of change of the total momentum will be equal to the net external force on the system.

\begin{equation} \frac{d\vec P_{\text{system}} }{dt} = \vec F_{\text{net}}^{\text{ext}},\tag{7.46} \end{equation}

where $\vec F_{\text{net}}^{\text{ext}}$ is the vector sum of external forces on all particles of the multiparticle system.

\begin{equation*} \vec F_{\text{net}}^{\text{ext}} = \vec F_1^{\text{ext}} + \vec F_2^{\text{ext}} + \cdots + \vec F_N^{\text{ext}}. \end{equation*}

Subsection 7.5.3 Center of Mass Motion

Another useful interpretation of the rate of change of total momentum equation, Eq. (7.46), is that it represents the motion of a mathematical particle of mass equal to the total mass of the system located at a special point in space called the center of mass or CM of the system as we will see below. The center of mass point does not have to be anywhere in the body or bodies making up the multiplarticle system. For instance, the center of mass of a ring, whose mass is spread out uniformly around the ring, is at the center of the ring where no particle of the ring is located.

Consider a system consisting of $N$ particles of masses $m_1\text{,}$ $m_2\text{,}$ $\cdots\text{,}$ $m_N\text{,}$ whose position vectors with respect to some origin are given by $\vec r_1\text{,}$ $\vec r_2\text{,}$ $\cdots\text{,}$ $\vec r_N$ respectively as shown in Figure 7.57.

Figure 7.57. The location of the center of mass (CM) of an N-particle system is obtained mass-weigting the positions of each vector as shown in Eq. (7.48).

Let $M$ be the total mass of the system,

\begin{equation*} M = m_1 + m_2 + \cdots + m_N. \end{equation*}

The position vector of center of mass (CM) of the system, to be denoted by $\vec R_{\textrm{cm}}\text{,}$ is defined by mass-weighting the position vectors of all the particles.

\begin{equation} M\vec R_{\textrm{cm}} = m_1 \vec r_1+ m_2 \vec r_2+ \cdots + m_N\vec r_N,\tag{7.47} \end{equation}

or,

\begin{equation} \vec R_{\textrm{cm}} = \frac{m_1 \vec r_1+ m_2 \vec r_2+ \cdots + m_N\vec r_N}{M}.\tag{7.48} \end{equation}

Taking derivative with respect to time on both sides of Eq. (7.47) we see that the momentum of a particle of mass $M$ moving with $R_{\textrm{cm}}$ is equal to the total momentum of the system.

\begin{equation} M \frac{d\vec R_{\textrm{cm}}}{dt} = m_1 \frac{d\vec r_1}{dt}+ m_2 \frac{d\vec r_2}{dt}+ \cdots + m_N\frac{d\vec r_N}{dt},\tag{7.49} \end{equation}

or,

\begin{equation} M \vec V_{\textrm{cm}} = m_1 \vec v_1+ m_2 \vec v_2+ \cdots + m_N\vec v_N,\tag{7.50} \end{equation}

where we have defined the center of mass velocity by the rate of change of the center of mass position vector.

\begin{equation} \vec V_{\textrm{cm}} = \frac{d\vec R_{\textrm{cm}}}{dt}.\tag{7.51} \end{equation}

Define the center of mass momentum $\vec P_{cm}$ as the momentum of a fictitious particle of mass equal to the total mass of the system and moving with center of mass velocity.

\begin{equation} \vec P_{\textrm{cm}} = M \vec V_{\textrm{cm}}.\tag{7.52} \end{equation}

Then, we have the result that the center of mass momentum is equal to the sum of the momenta of all particles in the system.

\begin{equation} \vec P_{\textrm{cm}} =\vec p_1 + \vec p_2 +\cdots + \vec p_N = \vec P_{\textrm{system}}\tag{7.53} \end{equation}

The acceleration of the center of mass is defined by the derivative of the velocity of the CM.

\begin{equation} \vec A_{\textrm{cm}} = \frac{d\vec V_{\textrm{cm}}}{dt}.\tag{7.54} \end{equation}

Using the result given in Eq. (7.46), we can now write the equation of motion of the center of mass as follows.

\begin{equation} \vec F_{\textrm{net}}^{\textrm{ext}} = \frac{d\vec P_{\textrm{cm}}}{dt},\tag{7.55} \end{equation}

which for a constant mass system becomes

\begin{equation} \vec F_{\textrm{net}}^{\textrm{ext}} = M \vec A_{\textrm{cm}}.\tag{7.56} \end{equation}

Equations (7.55) and (7.56) give the translational motion of the system as a whole since the system has been replaced by one point particle of total mass moving with the center of mass. The detailed information about the motions of individual particles has been lost since the motion of any particle depends on both the external forces and the internal forces on that particle.

For instance, if a system consists of two particles of equal mass moving in opposite directions, then we will find that center of mass is at rest. In this example, just because the center of mass is at rest does not imply no motion is taking place in the system. The detailed motion of each particle requires the study of the equations of motion of each particle separately.

Remark 7.58. Recap:.

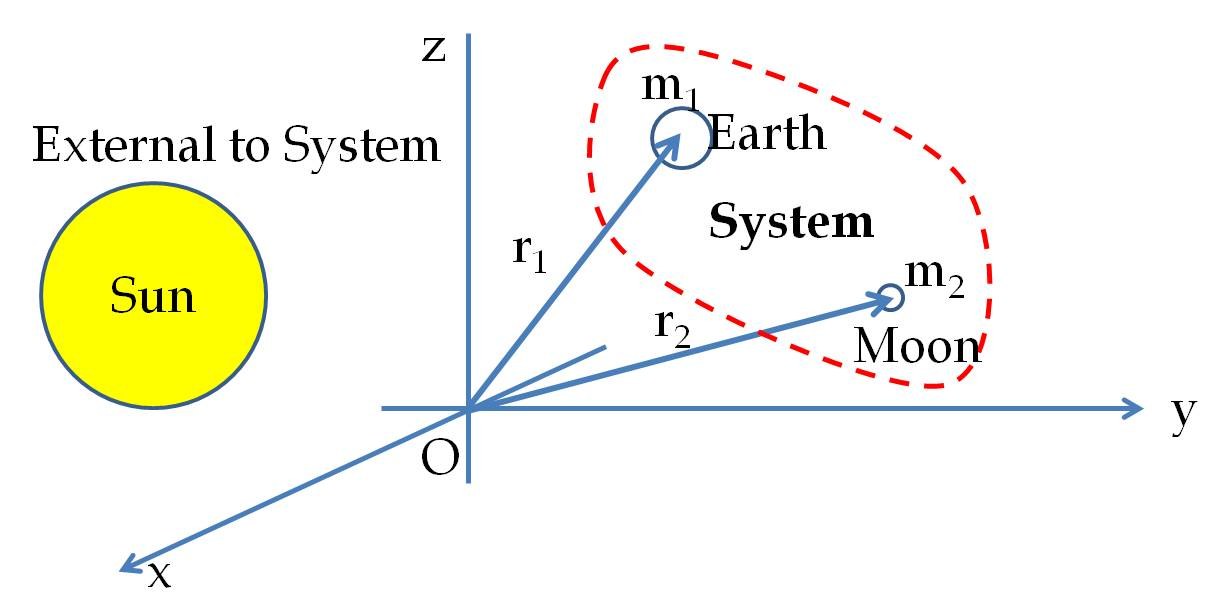
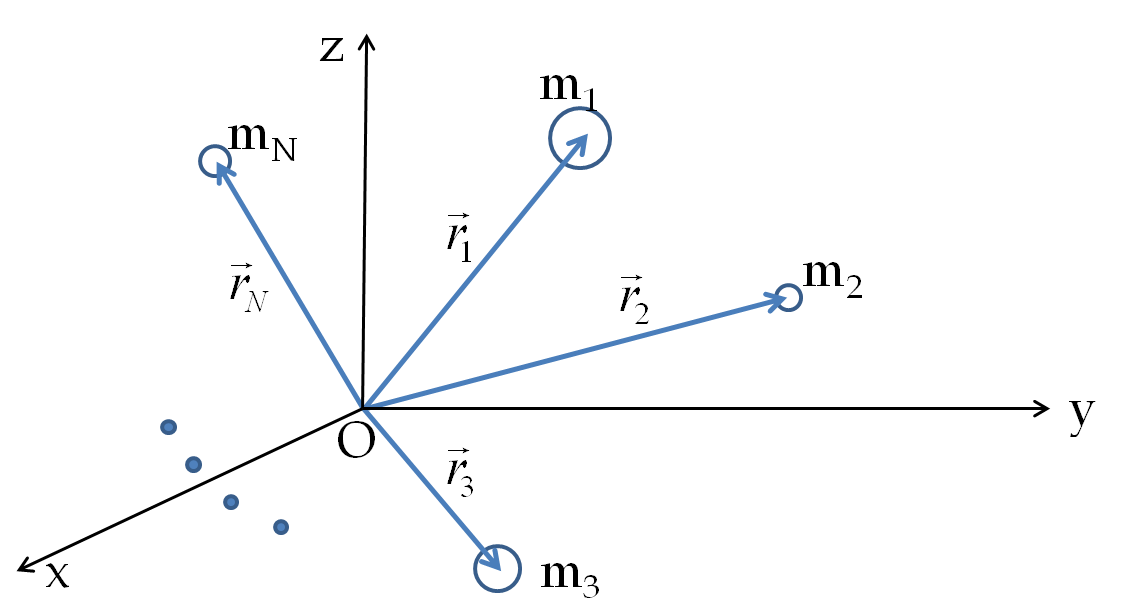
Center of mass of an object provides an important way to follow the overall motion of the object. We have already seen the formula for the position of the center of mass. For a body that is a collection of discrete masses $m_1$ at $\vec r_1\text{,}$ $m_2$ at $\vec r_2\text{,}$ $\cdots\text{,}$ $m_N$ at $\vec r_N\text{,}$ the center of mass will be at $\vec R_\text{CM}\text{,}$ given by

\begin{equation} \vec R_\text{CM} = \frac{1}{M}\left( m_1\vec r_1 + m_2\vec r_2 + \cdots + m_N\vec r_N \right),\tag{7.57} \end{equation}

where total mass $M=m_1+m_2+\cdots+m_N$ and $\vec r_i$ actually refer to the center of mass of the $i^\text{th}$ part. Now, studying the rate at which the center of mass $\vec R_\text{CM}$ changes will give us the velocity of center of mass, $\vec V_{\text{CM}}\text{.}$ Taking a time derivate of both sides, it is immedeiately clear that

\begin{equation} \vec V_{\text{CM}}\equiv \frac{d \vec R_\text{CM}}{dt} = \dfrac{m_1\vec v_1 + m_2\vec v_2 + \cdots + m_N\vec v_N }{M}.\tag{7.58} \end{equation}

Similarly, when we look at the rate which $\vec V_{\text{CM}}$ changes, we get the acceleration of the center of mass, $\vec A_{\text{CM}}\text{.}$ By taking one more derivative gives

\begin{equation} \vec A_{\text{CM}}\equiv \frac{d \vec V_\text{CM}}{dt} = \dfrac{m_1\vec a_1 + m_2\vec a_2 + \cdots + m_N\vec a_N }{M}. \tag{7.59} \end{equation}

The total momentum of all particles will be

\begin{equation*} \vec p_\text{total} = m_1\vec v_1 + m_2\vec v_2 + \cdots + m_N\vec v_N. \end{equation*}

Now, this is just $M \vec V_{\text{CM}}$ as you can see from Eq. (7.58) when you multiply it by $M\text{.}$

\begin{equation*} M \vec V_{\text{CM}} = m_1\vec v_1 + m_2\vec v_2 + \cdots + m_N\vec v_N \end{equation*}

We call the product $M \vec V_{\text{CM}}$ the center of mass momentum, $\vec P_{\text{CM}}\text{,}$ which is actually equal to the total momentum of all particles in the body.

\begin{equation} \vec P_{\text{CM}} = M \vec V_{\text{CM}} = \vec p_1 + \vec p_2 + \cdots + \vec p_N = \vec p_\text{total}. \tag{7.60} \end{equation}

Subsection 7.5.4 Center of Mass Motion - Constant Mass Case

Let us consider a system with $N $ parts of masses $m_1 \text{,}$ $m_2 \text{,}$ $\cdots \text{,}$ $m_N \text{.}$ Let $\vec F_1 \text{,}$ $\vec F_2 \text{,}$ $\cdots \text{,}$ $\vec F_N $ be forces acting on those parts. For the sake of simplicity, let us look at the constant mass system, i.e., where masss of each part is fixed in time.

Now, we write Newton’s equation of motion for each part for constant mass.

\begin{align*} \amp \vec F_1 = m_1 \vec a_1 \\ \amp \vec F_2 = m_2 \vec a_2 \\ \amp \cdots \\ \amp \vec F_N = m_N \vec a_N \end{align*}

Summing them, we find that the left side can be written as sum over all the forces from objects outside the $N $ parts making up the system, which we call the external forces $\vec F_{\text{net}}^{\text{ext}}\text{,}$ and a sum over all the forces that one part applies on another part, wwhich we call the internal forces $\vec F_{\text{net}}^{\text{int}}\text{.}$

\begin{equation*} \text{Left Side } = \vec F_1 + \vec F_2 + \cdots + \vec F_N = \vec F_{\text{net}}^{\text{ext}} + \vec F_{\text{net}}^{\text{int}} \end{equation*}

In this expression, internal forces, say by part 1 on 2 and by part 2 on 1 come in pairs, which by Newton’s third law must sum to zero. Therefore, we will have

\begin{equation*} \vec F_{\text{net}}^{\text{int}} = 0. \end{equation*}

That gives us the following simplified equation after summing the equations of all $N $ parts.

\begin{equation*} F_{\text{net}}^{\text{ext}} = m_ 1\vec a_1 + m_2\vec a_2 + \cdots + m_N\vec a_N, \end{equation*}

whose right side is just the total mass $M $ times the center-of-mass acceleration $\vec A_{\text{CM}} \text{.}$

\begin{equation} F_{\text{net}}^{\text{ext}} = M \vec A_{\text{CM}}.\tag{7.61} \end{equation}

It is interesting that the overall motion of a malti-part system can be captured essentially by the motion of a single (fictitious) particle of total mass placed at the center of mass. This is the equation we solve whenever we study the overall translation motion of finite-size objects since they are inherently mutiparticle systems.

General Case (Calculus):

We have seen before that the general case of mass varying as well as constant mass systems is given in terms of rate of change of momentum.

\begin{equation*} \vec F = \frac{d\vec p}{dt}. \end{equation*}

Now, if you apply this to the $N$-particle system, you will get

\begin{equation*} F_{\text{net}}^{\text{ext}} = \frac{d\vec P_\text{CM}}{dt} = \frac{d\vec p_\text{total}}{dt}. \end{equation*}

Similarly, the integrated form in terms of impulse and change in momentum will be

\begin{equation} \vec J_{\text{net}}^{\text{ext}}= \int F_{\text{net}}^{\text{ext}} dt = \vec p_{\text{total},f} - \vec p_{\text{total},i},\tag{7.62} \end{equation}

i.e., the change in momentum over the interval $i\rightarrow f$ is equal to the net impulse by only the external forces on various parts of the body.

Example 7.59. CM of an exploding shell.

As an example consider the motion of pieces of an exploded shell in free-fall.

Although the pieces fly away in various directions, the CM falls as if no explosion had taken place since during the explosion all forces are internal to the system. The motion of CM is that of a single particle with total mass of the system. The fictitious particle at the CM falls freely with acceleration equal to g, the acceleration due to gravity, until one of the pieces hits the ground.

At the instant first piece hits the ground, there will be a new upward impulse on the collective body. That is, the CM’s free fall motion will end.

Example 7.60. The Motion of the Center of Mass of a Diver.

A diver jumps off a board with initial speed $12\text{ m/s}$ at an angle $60^\circ$ with the horizontal direction. She falls a total height of $8\text{ m}$ before entering water. Find the speed of her center of mass when she enters water?

Answer.

$17.4\text{ m/s}\text{.}$

Solution.

Since the only force on her body after she takes off is her weight. The CM will obey the free fall equations. Therefore, we start with components of her initial velocity.

\begin{align*} v_{ix} \amp = 12\,\cos\,60^{\circ} = 6\text{ m/s}, \\ v_{iy} \amp = 12\,\sin\,60^{\circ} = 10.4\text{ m/s}. \end{align*}

The final $v_x$ is same as the initial, and the final $v_y$ is obtained from

\begin{equation*} v_{fy} = - \sqrt{ v_{iy}^2 - 2 g \Delta y}, \end{equation*}

where $\Delta y = - 8\text{ m}\text{,}$ which is negative since the final location is below the initial point, and $v_{fy}$ is negative since it is pointed down while positive $y$ axis is pointed up.

\begin{equation*} v_{fy} = -\sqrt{ 10.4^2 + 2\times9.81\times 8} = -16.3\text{ m/s}. \end{equation*}

From $v_{fx}$ and $v_{fy}$ we get the speed just before she enters water.

\begin{equation*} v_f = \sqrt{ v_{fx}^2 + v_{fy}^2 } = \sqrt{6^2 + 16.3^2} = 17.4\text{ m/s}. \end{equation*}

Example 7.61. Impulse for a Vertical Jump.

A $78.0\text{-kg}$ athlete jumps straight up so that his CM moves by a height of $1.2\text{ m}$ after he leaves the ground. Find the magnitude of impulse from the ground.

Answer.

$378.3\text{ N.s}\text{.}$

Solution.

The jump is due to push by the athlete on the ground which causes a normal force that exceeds his weight and gives upward momentum when he leaves the ground. This force from the ground during the jumping process is responsible for imparting initial upward momentum.

Let $v_0$ be the velocity pointed upwards at the instant athlete leaves the ground and $m$ mass of the athlete. Then, the change in momentum from zero to $mv_0$ will equal the the impulse by ground. Let us work with $y$ axis pointed up. Then, $y$-component of impulse will be

\begin{equation*} J_y = \Delta p_y = mv_0., \end{equation*}

The CM starts with velocity $v_0$ and has constant acceleration under the external force of gravity so that its velocity is zero at maximum height $h\text{.}$ Using constant acceleration of the motion of CM along $y$ axis we get

\begin{equation*} 0 - v_0^2 = - 2 g h\ \ \longrightarrow\ \ v_0 = \sqrt{2gh}. \end{equation*}

Hence, impulse by ground is

\begin{equation*} J = m\sqrt{2gh} = 78\sqrt{2\times 1.2\times 9.8} = 378.3\text{ N.s}. \end{equation*}

Example 7.62. Speed When Jumping Off Vertically.

Suppose you are trying to practice a vertical jump. You crouch down and push against the ground.

The magnitude of the normal force from the ground on you varies with time as shown in Figure 7.63 of $F$ versus $t\text{.}$ The initial normal force is just your weight. As you push down, the normal force increases. You leave the ground at the point normal force is zero.

As a net result of normal force from the ground, and weight, your center of mass has acceleration upward. What will be your speed at the instant you are no longer in contact with the ground?

Answer.

$1.47\text{ m/s}.$

Solution.

Let positive $y$ axis be pointed up. We will implement the following law for the center of mass since CM momentum is equal to $p_\text{tot}\text{.}$

\begin{equation*} J_y^{\text{net}} = \Delta p_y^{CM}. \end{equation*}

To get the net impulse, we need to vectorially add up impulses from all forces on the body. We have two forces on the body here - the weight and the normal force. From $t=0$ point in Figure 7.63, we note that magnitude of weight is $500\text{ N}\text{.}$ Since weight has negative $y$ component, its $J_y$ will be negative.

\begin{equation*} J_y^{\text{weight}} = - 500\text{ N}\times 0.200\text{ s} = -100\text{ N.s}. \end{equation*}

The impulse from the normal force is the area under the given plot.

\begin{align*} J_y^{\text{normal}} \amp = \left( 500\times 0.2 - \dfrac{500\times 0.02}{2}\right) \\ \amp \ \ \ \ + \dfrac{1000\times 0.08}{2} + 1000\times 0.02 + \dfrac{1000 \times 0.04}{2}, \\ \amp = 175\text{ N.s}, \end{align*}

which is obtained by slicing the area into triangles and rectangle. Therefore,

\begin{equation*} J_y^{\text{net}} = 175\text{ N.s} - 100\text{ N.s} = 75\text{ N.s}. \end{equation*}

The mass of the person is obtained from the weight.

\begin{equation*} m = \dfrac{500\text{ N}}{9.81\text{ m/s}^2} = 51\text{ kg}. \end{equation*}

Initially, the momentum was zero. Therefore, the velocity at the end is

\begin{equation*} v_{\text{cm}} = \dfrac{75\text{ N.s}}{51\text{ kg}} = 1.47\text{ m/s}. \end{equation*}

Exercises 7.5.5 Exercises

1. Motion of Center of Mass of Two Blocks Attached by a Spring.

Two blocks of mass $m$ each is attached by a spring of spring constant $k$ and unstretched length $l_0\text{.}$ The blocks are placed on a horizontal frrictionless track.

While holding one of the blocks, say B in the figure, the other block is pushed in so that spring compresses by $D\text{,}$ and then everything is released from rest at $t=0\text{.}$ Use $x$-axis so that at $t=0\text{,}$ $x_A=D$ and $x_B=l_0\text{.}$

Find the position of the center of mass, $x_\text{cm}\text{,}$ at an arbitrary instant $t\text{.}$

Hint.

Since there is no external force, $x_\text{cm}$ will remain fixed in time. You can show this by a detailed calculation.

Answer.

$x_\text{cm} (t)= \frac{D+l_0}{2}\text{.}$

Solution.

Since there is no external force, $x_\text{cm}$ will remain fixed in time. Since the center of mass is at $x=(D+l_0)/2$ at $t=0\text{,}$ it will remain there. This does not mean A and B do not move - they do, but their CM remains at the same point in space. We can also show this by a detailed calculation as follows.

Figure 7.65 shows situation at an arbitrary instant when the spring is stretched. The spring forces on the two blocks are shown.

The $x$-equations of motion for the two blocks will be

\begin{align} \amp m_A\frac{d^2x_A}{dt^2} = k (x_B - x_A - l_0) \tag{7.63}\\ \amp m_B\frac{d^2x_B}{dt^2} = -k (x_B - x_A - l_0) \tag{7.64} \end{align}

Here $m_A=m_B=m$ and $x_B \gt x_A\text{.}$ Since center of mass is give by

\begin{equation*} x_\text{cm} = \frac{1}{2}\left( x_A + x_B \right), \end{equation*}

we can take two derivatives with respect to time to get

\begin{equation*} \frac{d^2x_\text{cm}}{dt^2}= \frac{1}{2}\left( \frac{d^2x_A}{dt^2} + \frac{d^2x_B}{dt^2} \right). \end{equation*}

Using the equations of motions for $x_A$ and $x_B\text{,}$ we immediately get

\begin{equation*} \frac{d^2x_\text{cm}}{dt^2} = 0. \end{equation*}

This has a simple solution.

\begin{equation} x_\text{cm}(t) = a t + b,\tag{7.65} \end{equation}

where $a$ and $b$ will be fixed from the initial conditions.

\begin{equation*} x_A=D,\ \ x_B = l_0,\ \ v_A = 0 ,\ \ v_B=0. \end{equation*}

Writing Eq. (7.65) in terms of $x_A$ and $x_B$ and also writing their derivative we have

\begin{align*} \amp \frac{1}{2}\left( x_A + x_B \right) = a t + b\\ \amp \frac{1}{2}\left(v_A + v_B \right) = a \end{align*}

Evaluating these at $t=0$ we get

\begin{equation*} a = 0,\ \ b = \frac{D+l_0}{2}. \end{equation*}

Therefore, we have the following answer for the center of mass at arbitrary instant $t\text{.}$

\begin{equation} x_\text{cm} = \frac{D+l_0}{2}.\tag{7.66} \end{equation}

That is, CM remains fixed at $x= (D+l_0)/2\text{.}$

2. (Calculus) Motion of Center of Mass of Two Blocks Attached by a Spring with One Block Piushed Against a Wall.

In Exercise 7.5.5.1, the two blocks moved freely on the frictionless horizontal track.

Now, suppose you were pushing block A, you kept block B against a wall as shown in Figure 7.66.

After compressing the spring by amount $D\text{,}$ you release both blocks at rest. What will be the motion of the center of mass if $l_0$ is the natural length of the spring?

Hint.

First solve the situation when block B is in contact with the wall. Then solve the situation after B loses contact with the wall. When in contact, set up equation of motion for the CM and another equation of motion for B. Also, use the relation between $x_A$ and $x_\text{cm}\text{.}$

Answer.

Solution.

Overall strategy:

The motion of the center of mass will be controlled by external forces on the two-block (and spring) system. When block B is in contact with the wall, the net external force on the two-block system comes from the normal force of the wall, which will vary with the varying length of the spring. When block B is no longer in contact with the wall, the normal force from the wall will be zero, which will make net external force zero on the two block system. Thus, after block B is no longer in contact with the wall, the center of mass will just move with a constant velocity.

Block B in Contact with the Wall:

Figure 7.67 shows situation at an arbitrary instant when block B is still in contact with the wall. The equation of motion of the center of mass will be

\begin{equation*} M \frac{d^2x_\text{cm}}{dt^2} = - N(t). \end{equation*}

We need an expression for $N(t)$ to solve this equation. We get that by looking at force on B as shown in Figure 7.68. Balancing spring and wall forces on B gives

\begin{equation*} N(t) = k (l_0 - x_A). \end{equation*}

We also note that when B is at the wall $x_\text{cm}$ and $x_A$ are related by

\begin{equation*} x_\text{cm} = \frac{m x_A + m l_0}{2m} = \frac{x_A + l_0}{2}. \end{equation*}

Using the three equations above, we get the following equation of motion for $x_\text{cm}\text{.}$

\begin{equation*} \frac{d^2x_\text{cm}}{dt^2} = \frac{k}{m}\left(x_\text{cm} - l_0\right). \end{equation*}

This has the following general solution.

\begin{equation} x_\text{cm}(t) = l_0 + A\, e^{\sqrt{k/m}\, t} + B\, e^{-\sqrt{k/m}\, t}.\tag{7.67} \end{equation}

The velocity of CM will be

\begin{equation} v_\text{cm}(t) = \sqrt{k/m}\,A\, e^{\sqrt{k/m}\, t}- \sqrt{k/m}\,B\, e^{-\sqrt{k/m}\, t}.\tag{7.68} \end{equation}

Using the initial conditions on A and B, we have the following intial conditions on CM.

\begin{align*} \amp x_\text{cm}(t) = \frac{x_A (0)+ l_0}{2} = \frac{D+ l_0}{2}.\\ \amp v_\text{cm}(t) = \frac{v_A (0)}{2} = 0. \end{align*}

Using these in Eqs. (7.67) and (7.68), we find

\begin{equation*} A = B = \frac{D-l_0}{4}. \end{equation*}

Therefore, the position of CM and its velocity are

\begin{align} \amp x_\text{cm}(t) = l_0 - \left(\frac{l_0-D}{2} \right)\,\cosh(\sqrt{k/m}\,t). \tag{7.69}\\ \amp v_\text{cm}(t) = -\frac{(l_0-D)\sqrt{k/m}}{2}\,\sinh(\sqrt{k/m}\,t).\tag{7.70} \end{align}

Block B not in Contact with the Wall:

At the instant, block B loses contact with the wall, the CM will be at $l_0/2\text{.}$ At that instant onward the velocity of the CM will remain unchanged since there are net external force on the two-block system is zero now. We can find the time when this happens from Eq. (7.69). Let this instant be at $t=T\text{.}$

\begin{equation*} \frac{l_0}{2} = l_0 - \left(\frac{l_0-D}{2} \right)\,\cosh(\sqrt{k/m}\,T) \end{equation*}

Therefore,

\begin{equation*} T = \sqrt{\frac{m}{k}}\, \cosh^{-1}\left( \frac{l_0}{l_0 - D} \right). \end{equation*}

From Eq. (7.70), the velocity of CM after this instant will be constat at

\begin{align*} v_\text{cm}(t>T)\amp = - \frac{(l_0-D)\sqrt{k/m}}{2} \,\sinh(\sqrt{k/m}\,T)\\ \amp = -\frac{(l_0-D)\sqrt{k/m}}{2}\,\sinh\left[ \cosh^{-1}\left( \frac{l_0}{l_0 - D} \right) \right]. \end{align*}

This expression can be simplified by noting that

\begin{equation*} \sinh(\cosh^{-1}(x)) = \sqrt{x^2 - 1}. \end{equation*}

To prove this try $y=\cosh^{-1}(x)$ and solve for $e^y = x + \sqrt{x^2-1}$ and $e^{-y} = x - \sqrt{x^2-1}\text{.}$ Using this, we simplify CM velocity for $t\gt T$ to be

\begin{equation*} v_\text{cm}(t>T) = -\frac{1}{2}\sqrt{ \frac{k}{m} (2l_0 D - D^2) }. \end{equation*}

The velocity is $x$-component and pointed towards negative $x$-axis. That is why there is a negative sign in the front.

Prev Top Next