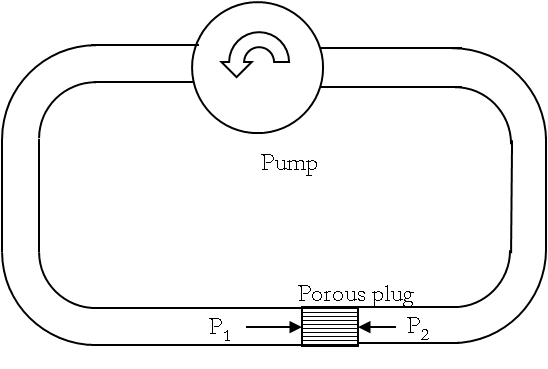
Imagine pumping a gas through a thermally insulated tube that has a porous plug such that the pressure on the two sides of the plug is different. Let
\(p_1\) be the pressure on one side of the plug and a different pressure
\(p_2\) on the other side as shown in
Figure 24.24. We will take
\(p_1 \gt p_2\) for the discussion below. Let the pressure on each side be maintained steady by a pump and the entire system be thermally insulated. The process of pumping a gas this way is called
Joule-Thomson process or
Joule-Thomson throttling.
The throttling process does not occur slowly or quasi-statically. However, we can still apply the first law of thermodynamics to obtain important conclusions about this process. Since the system is thermally insulated, the change in internal energy \(U_2-U_1\) of the gas will be equal to the negative of the amount of work done by the gas in this nonquasistatic process. How do we calculate the work done by the gas here since we do not have \(p(V)\) for the process? We take a different approach as follows.
The trick is to imagine a process in which we empty \(n\) moles of gas occupying a volume \(V_1\) while keeping the pressure at \(p_1\) all the time. Let \(W_1\) be the work done by the gas in this process. And, then we fill a volume \(V_2\) of space with \(n\) moles of gas at pressure \(p_2\text{.}\) Let the work done by the gas in this process by \(W_2\text{.}\) The net work by the gas will be
\begin{equation*}
W_{\textrm{net}} = W_1 + W_2.
\end{equation*}
The works \(W_1\) and \(W_2\) are readily calculated since they are constant pressure processes with the following results.
\begin{align*}
\amp W_1 = - p_1V_1\\
\amp W_2 = p_2V_2
\end{align*}
Hence the change in the internal energy of the gas under consideration is
\begin{equation*}
U_2 - U_1 = p_1V_1 - p_2 V_2.\ \ \ \textrm{(thermally insulated)}
\end{equation*}
Rearranging, we find that in the Joule-Thompson process the combination, \(U+pV\text{,}\) is conserved.
\begin{equation}
U_2 + p_2 V_2 = U_1 + p_1V_1 \ \ \ \textrm{(Joule-Thomson process)}\tag{24.32}
\end{equation}
As you may recall, the quantity \(U+pV\) is called enthalpy or heat function \(H\text{.}\) It is a state function similar in status to the internal energy \(U\text{.}\)
\begin{equation*}
H = U + p V.\ \ \textrm{Definition of enthalpy}
\end{equation*}
A process that conserves enthalpy is called iso-enthalpic process. The Joule-Thompson process conserves enthalpy. Comparing the final enthalpy and initial enthalpy we can conclude that if pressure times volume goes up, then internal energy must go down and vice-versa. Joule-Thompson throttling is often used in cooling and liquefying gases.