Viscosity

Section 18.4 Viscosity

Subsection 18.4.1 Cohesive Forces and Laminar Flow

Real liquids slow down in their flow unless some energy is continuously pumped in the liquid. The source of dissipation of energy are the intermolecular or cohesive forces. Energy of in the flow is converted into thermal energy which escapes to the environment or heats up the fluid. We will also call these forces viscous forces.

It is possible to learn about the viscous cohesive forces inside the liquid by applying a shear force tangentially on the liquid surface. The fluid will flow, but, when you stop applying the external force, the flow will slow down due to the work by the internal viscous forces. For instance, when a wind blows over the surface of a lake, the water flows, and when the wind stops, the flow also stops due to the dissipation of energy by way of heat.

When the wind is blowing over a lake, the speed of flow at the surface is more than the flow deeper down in the water. If you assume a laminar flow model of a fluid, then we can study the flow of the fluid layer by layer by assuming that fluid in each layer flows at the same speed. The laminar flow with one surface fixed and the opposite surface subjected to a shear stress will give rise to varying speeds of the layers due to the viscous forces in the liquid as shown in Figure 18.23.

Figure 18.23. *Laminar flow model*. Fluid is modeled as layers with each layer flowing at its speed and different layers flow at different speeds. In this figure, the top layer is pushed along by a shear force at a higher spped and the bottom layer is next to a fixed plate.

Subsection 18.4.2 Laminar Flow

Consider the following experiment. Place some liquid between two flat plates separated by a distance \(h\) as shown in Figure 18.24. Keeping the bottom plate fixed, we apply a constant horizontal force \(F\) on the top plate to make the top surface move at a steady speed \(v_{\text{top}}\) while the bottom layer remains at rest.

Figure 18.24. Shear strain \(\Delta \theta\) under a shear stress \(F/A\) in a duration \(\Delta t\text{.}\) Force \(F \) is balanced by the viscous force \(F_{\text{visc}}\) at the top, not shown. While the top layer moves with speed \(v \text{,}\) bottom layer has zero speed.

Experiments show that the horizontal force \(F\) needed to maintain a steady speed \(v_{\text{top}}\) of the top plate is directly proportional to the contact area \(A = w l\) and the speed \(v_\text{top}\) of the top plate relative to the fixed plate, and inversely proportional to the distance \(h\) between the plates.

\begin{equation} F = \eta A \frac{v_\text{top}}{h},\tag{18.28} \end{equation}

where the constant of proportionality \(\eta\) (the Greek letter “eta”) is called the coefficient of viscosity, or simply viscosity. The viscosity force in the fluid just below the top plate is equal to this force, since we pull on the top surface at constant velocity.

\begin{equation} F_\text{visc,top} = F = \eta A \frac{v_\text{top}}{h},\tag{18.29} \end{equation}

where

\begin{equation*} v_\text{top} = \dfrac{ \Delta x _{\text{top}} }{\Delta t} \approx \dfrac{ h\Delta \theta}{\Delta t}. \end{equation*}

From the geometry in Figure 18.24 we can tell that the displacemnt in time \(\Delta t\) of flow in layer at height \(z = z \text{,}\) we know

\begin{equation*} \Delta x = z\, \Delta \theta, \end{equation*}

which gives the following for the speed of flow in that layer.

\begin{equation*} v(z) = \dfrac{\Delta x}{\Delta t} = \dfrac{z}{h}\, v_\text{top}. \end{equation*}

Therefore, the viscous force at this layer is

\begin{equation} F_\text{visc}(z) = \eta A \dfrac{z}{h} v_\text{top}.\tag{18.30} \end{equation}

That is layer speeds increase from zero to \(v_{\text{top}}\text{.}\)

Subsection 18.4.3 Units of Coefficient of Viscosity

The viscosity coefficient has dimensions of \([M]/[L][T] \) as determined from the dimensions of other quantities in Eq. (18.30).

\begin{equation*} [\eta] = \frac{[F][h]}{[A][v]} = \frac{[M]}{[L][T]}. \end{equation*}

The unit of the coefficient of viscosity in SI-system is \(\text{Pa.s}\text{,}\) which is also called poiseuille (\(\text{PI}\)) after Jean Louis Marie Poiseuille (1797-1869). A more common unit of viscosity is the unit in the centimeter-gram-second-system of units. That unit is called poise, which is equal to \(1\text{ dyne.sec/cm}^2\text{,}\) where \(\text{dyne}\) is the unit of force in that system, \(\text{dyne} = \text{g.cm/s}^2\text{.}\) The relation between the two system of units are:

\begin{equation*} 1\text{ poise} = 0.1\text{ Pa.s} = 0.1\text{ PI} \end{equation*}

The viscosity of many common fluids are usually tabulated in centipoise.

Subsection 18.4.4 (Calculus) Velocity of the Layers in Laminar Flow - Rectangular Geometry

In Subsection 18.4.2, we have already discussed an overall picture of laminar flow when we apply a tangential stress on a rectangular shaped fluid. Here we dig a little deeper.

For analytic treatment, we use the coordinate system in Figure 18.24, reproduced here in Figure 18.25 where the flow is in the direction of \(x \) axis and \(x\)-axis-directed external force \(F \) is at the top of a rectangularly shaped liquid body which sits on support at rest.

Figure 18.25. Shear strain \(\Delta \theta\) under a shear stress \(F/A\) in a duration \(\Delta t\text{.}\) Force \(F \) is balanced by the viscous force \(F_{\text{visc}}\) at the top, not shown. While the top layer moves with speed \(v \text{,}\) bottom layer has zero speed.

The layer at \(z+\Delta z\) has a force \(F_x^\text{above} \hat i\) from the layer above the \(z+\Delta z\) layer and layer at \(z\) has a force \(F_x^\text{below} \hat i\) from the layer below the \(z\) layer. The difference of the two forces must be balanced by inter-molecular forces since the fluid molecules between \(z\) and \(z+\Delta z\) have zero acceleration. We denote this force by \(\vec F_\text{visc,diff}\text{.}\) In the present experiment, we get the \(x\)-component of the this force to be

\begin{equation} F_x^\text{visc,diff} = F_x^\text{above} - F_x^\text{below} = \eta A \frac{\Delta v_x}{\Delta z},\tag{18.31} \end{equation}

where

\begin{equation*} \Delta v_x = v_x^\text{above} - v_x^\text{below}, \end{equation*}

and \(\Delta z\) is the thickness of the layer, which will now be treated as an infinitesimal. Taking \(\Delta z\rightarrow 0\) limit we find the following for \(F_x^\text{visc,diff}\) on the flow velocity \(v_x\) and the height \(z\) from a static layer. With \(\Delta z\rightarrow 0\) limit, we have removed the above and below, and found the internal force on the layer at \(z \text{.}\) Therefore, we remove the “diff” from the subscript of viscous force symbol.

\begin{equation} F_x^\text{visc} =\eta A \frac{dv_x}{d z}.\tag{18.32} \end{equation}

Note here, we get an \(x \) component of force, which is in the direction of the flow, based on the way the velocity changes with respect to the height coordinate \(z\text{.}\)

Many fluids, such as water, ethyl alcohol, glycerin, and most gases exhibit this simple linear dependence of shear on the gradient of velocity. They are called Newtonian fluids. When a fluid does not behave as postulated above, it is called a non-Newtonian fluid.

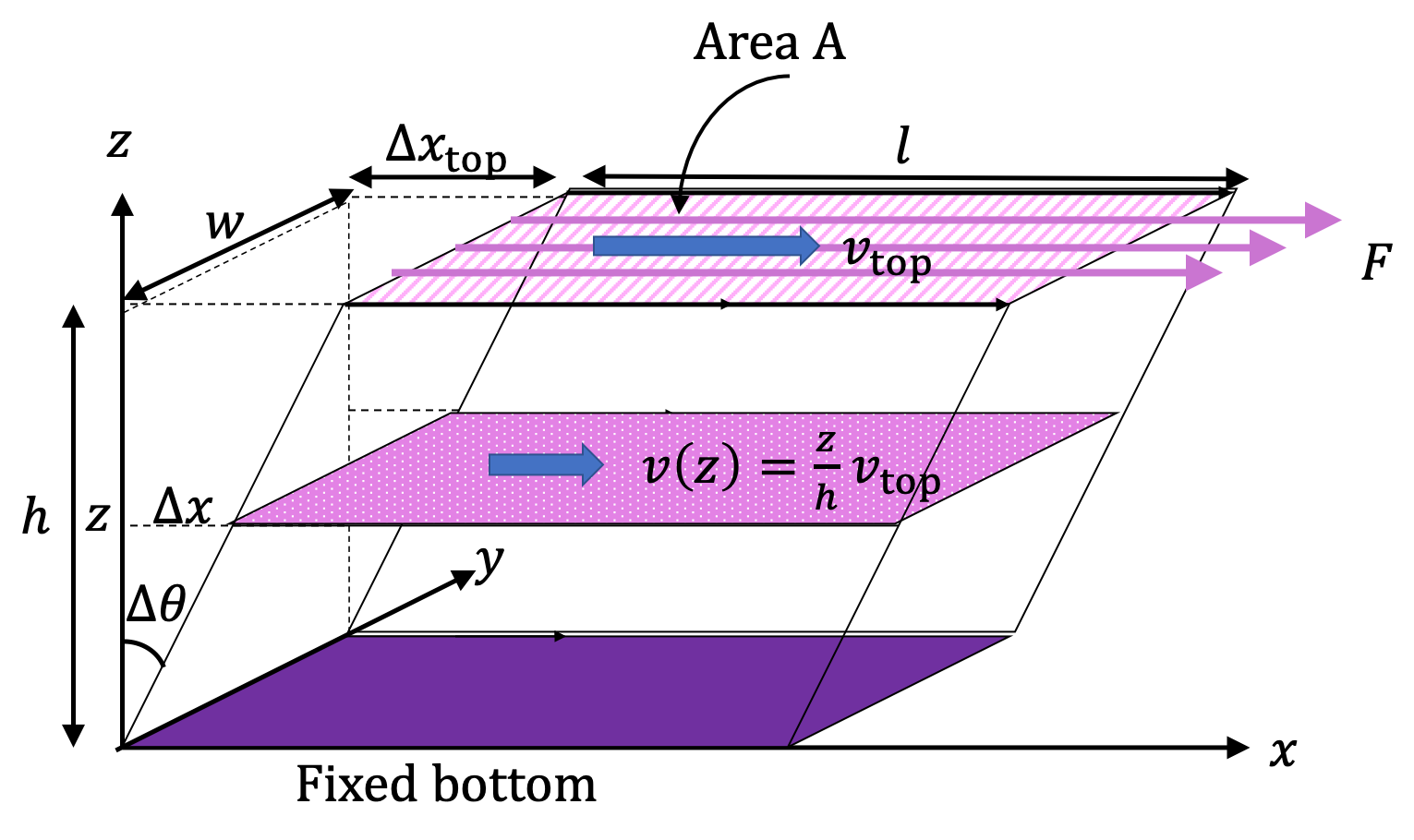
Example 18.26. Sliding Microscopic Slides with Liquid Between Them.

There is a \(0.8\text{-mm}\) thick layer of a bacterial culture medium fof viscosity \(0.95\text{ cP}\) between two \(5\text{ cm} \) long and \(2.5\text{ cm} \) wide microscopic slides. Assume the liquid is in the entire space between the slides.

(a) What force will you need to pull one slide over the other along the length at a speed of \(1.2\text{ cm/s}\text{?}\)

(b) What force will you need to pull one slide over the other along the width at a speed of \(1.2\text{ cm/s}\text{?}\)

Answer.

(a) \(1.78\times 10^{-6}\text{ N} \text{,}\) (b) Same magnitude as (a), direction is pependicular to that of (a).

Solution 1. a

We fix the lower slide and pull on the upper slide. We also need to convert units to the SI units before we use them in formulas.

\begin{align*} \amp h = 0.8\times 10^{-3}\text{ m},\\ \amp \eta = 0.95\text{ cP} = 0.95\times 10^{-4}\text{ Pa.s},\\ \amp A = 5\times 2.5\times 10^{-4}\text{ m}^2,\\ \amp v_{\text{top}} = 1.2\times 10^{-2}\text{ m/s}. \end{align*}

Therefore, the force between the plates is

\begin{align*} F \amp = \eta A \frac{v_\text{top}}{h},\\ \amp = 0.95\times 10^{-4} \times 7.5\times 10^{-4}\times \dfrac{1.2\times 10^{-2}}{0.8\times 10^{-3}},\\ \amp = 1.78\times 10^{-6}\text{ N}. \end{align*}

Solution 2. b

The only difference is the direction in which you will apply force. All other quantities are same.

Prev Top Next