Flux of Electric Field

Section 30.1 Flux of Electric Field

Flux of electric field is a measure of the strength of electric field over an area. In this section, we will define electric flux and learn to calculate electric flux from given a electric field. In the next section, we will show its use when we study Gauss’s law. To get a feel for the meaning of flux, we will first take a look at flux of particles.

Subsection 30.1.1 Flux of Particles

Imagine a stream of particles flowing through space as shown in Figure 30.1. We would like to know how many particles will strike a screen per unit time. This is called the particle flux through the area of the screen. Notice that flux changes with the orientation of the screen with respect to the flow - you get the most flux when area is facing perpendicularly to the flow.

Figure 30.1. Number of particles passing through a unit area surface per unit time is called particle flux. Notice that flux depends on the orientation of the surface to the direction of flow.

To work out a formula for the flux, let \(v \) be the speed of particles, \(A\) the area of the screen, and \(\rho\) the number density, i.e., number of particles per unit volume. Let’s first work out flux through an area that is perpendicular to the flow as A in Figure 30.1. In time \(\Delta t\text{,}\) all particles within a distance of \(v\Delta t\) would pass through the area. Number of particles in this volume, which is \(A\,v\,\Delta t\text{,}\) will be \(N = \rho\, v\, A\, \Delta t.\) Thenumber of particles per unit time passing the area \(A\) will be obtained by setting \(\Delta t = 1\) in this expression. This number is the particle flux, denoted by \(\Phi_\text{A}\text{.}\)

\begin{equation*} \Phi_\text{A} = \rho v A. \end{equation*}

But, when the orientation of the screen is as in C in Figure 30.1, assuming screen to be infinitesimally thin, no particle will strike the screen.

\begin{equation*} \Phi_\text{C} = 0 \end{equation*}

If the screen is oriented at some other angle, as in B, screen is effectively providing smaller area normal to the flow of the particles, and hence smaller effective area for particles to hit. From geometry, you can deduce that, in case of B in Figure 30.1, the effective area is only half as much.

\begin{equation*} A_\text{eff,B} = A \sin\,30^{\circ} = \frac{1}{2}A. \end{equation*}

Therefore, flux through B in Figure 30.1 will be

\begin{equation*} \Phi_\text{B} = \rho v A_\text{eff,B} = \frac{1}{2} \rho v A. \end{equation*}

In general, if area \(A\) is oriented at angle \(\phi\) with respect to the flow. Then, effective area is only

\begin{equation*} A_\text{eff} = A\sin\,\phi. \end{equation*}

The relative orientation is traditionally given by angle \(\theta\) between the flow and the normal to the area, with \(\theta=90^\circ-\phi\text{.}\) Therefore, effecive area is also

\begin{equation*} A_\text{eff} = A\cos\,\theta. \end{equation*}

Therefore, general formula for particle flux will be

\begin{equation*} \Phi = \rho v A_\text{eff} = \rho v A \sin\,\phi = \rho v A \cos\,\theta. \end{equation*}

Zero particle flux does not mean that there is no flow. Suppose you have steady flow of water in a U-shaped water pipe. The net flux of water molecules through the surface \(A\) will be zero since, if we take flux at \(A_1\) as positive, then flux at \(A_2\) will be negative, and they will cancel out when added to get flux through \(A\text{.}\)

Subsection 30.1.2 Flux of Electric Field

A visual way of thinking about the flux of elctric field is to think of it as a measure of number of electric field lines that passes through an area as illustrated in Figure 30.3.

Figure 30.3. Flux through an area is a measure of *number of electric field lines* through the area. In this figure, near point A, electric flux is 4 units and near B it is 2 units.

The analogy with the particle flux is that magnitude of the electric field, \(E\text{,}\) in the case of electric field will replace \(\rho v\) for particles. Therefore, we will have the following for electric flux.

\begin{equation} \Phi_E = E\, A_\text{eff},\tag{30.1} \end{equation}

where effecive area is the area projected on a plane perpendicular to the electric field. Writing this in terms of the area and orientation angle \(\theta\text{,}\) we get

\begin{equation} \Phi_E = E\, A \cos\, \theta.\tag{30.2} \end{equation}

Area Vector: Flux can be compactly written in vector notation if we introduce an area vector that takes into account its orientation. Let \(\hat u\) be normal to a flat area \(A\text{.}\) Then we call vector \(A\hat u\) an area vector and denote it by \(\vec A\text{.}\)

Using area vector \(\vec A \) and electric field vector \(\vec E\text{,}\) electric flux takes a compact form.

\begin{equation} \Phi_E = \vec E\cdot \vec A.\tag{30.3} \end{equation}

Zero electric flux does not mean that electric field is also zero.

Suppose we have a closed surface \(\text{S}\) near a positive electric charge. Every electric field line from positive charge that enters the surface at some point must exit at some other point. If you count exiting line as \(+1\) and entering line as \(-1\text{,}\) the net lines through the surface will be zero. That will give net flux zero, but clearly, electric field is not zero.

Subsection 30.1.3 (Calculus) Flux of Electric Field

Formula for electric field given in Eq. (30.3) works for uniform electric field and a single flat area. Now, we will like to extend this to arbitrary surface shape and arbitrary electric field. We still use Eq. (30.3) but use it on small patches of the surface, which can be approximated to be flat as illustrated in Figure 30.5.

Figure 30.5. Electric flux through a curved smooth surface is obtained by covering the surface with approximately flat patches. We find flux through each patch and then add them up to get the net flux.

Since any smooth surface can be covered by infinitesimal flat patches of area vectors, say \(\Delta \vec A\text{,}\) we compute flux through patches and add their contributions to obtain the net flux.

\begin{equation*} \Phi_E = \sum_\text{patches}\, \vec E\cdot \Delta\vec A. \end{equation*}

In the limit of \(\Delta\vec A\rightarrow 0\text{,}\) we write this formally as

\begin{equation} \Phi_E = \int_{\text{area}}\, \vec E\cdot d\vec A.\tag{30.4} \end{equation}

Often, we say that this is only a conceptual integral since you will have to convert area element \(d\vec A\) into appropriate form before you can actually get regular integrals for you to work out. For instance, suppose you have an area in \(xy\)-plane, your area element will be

\begin{equation} d\vec A = dx\,dy\,\hat k.\tag{30.5} \end{equation}

That will make the flux to

\begin{equation*} \Phi_E = \iint E_z dx dy, \end{equation*}

where \(E_z\) may be a function of \(x\) and \(y\) and the integration will be over the area.

On the other hand, if surface has spherical shape of radius \(r\text{,}\) the area element on that surface will be

\begin{equation} d\vec A = r^2\,\sin\,\theta\,d\theta\,d\phi\,\hat u_r,\tag{30.6} \end{equation}

where \(\hat u_r\) is a radially outward unit vector from origin to the location of the area element.

Therefore, for a spherical shape surface, flux will be

\begin{equation*} \Phi_E = r^2 \iint E_r\,\sin\,\theta\,d\theta\,d\phi, \end{equation*}

where \(E_r\) is the spherical radial component of the electric field, which may be a function of \(\theta\) and \(\phi\text{.}\)

If the surface has a cylindrical shape of radius \(r\) about the \(z\) axis, the area element will be

\begin{equation} d\vec A = r\,d\theta\,dz\,\hat u_r\tag{30.7} \end{equation}

where \(r\text{,}\) \(\theta\text{,}\) \(z\) are cylindrical coordinates and \(\hat u_r\) is a radially outward unit vector pependicular to the \(z\) axis.

Therefore, for a cylindrical shape surface, flux will be

\begin{equation*} \Phi_E = r \iint E_r\,\,d\theta\,dz, \end{equation*}

where \(E_r\) is the cylindrical radial component of the electric field, which may be a function of \(\theta\) and \(z\text{.}\)

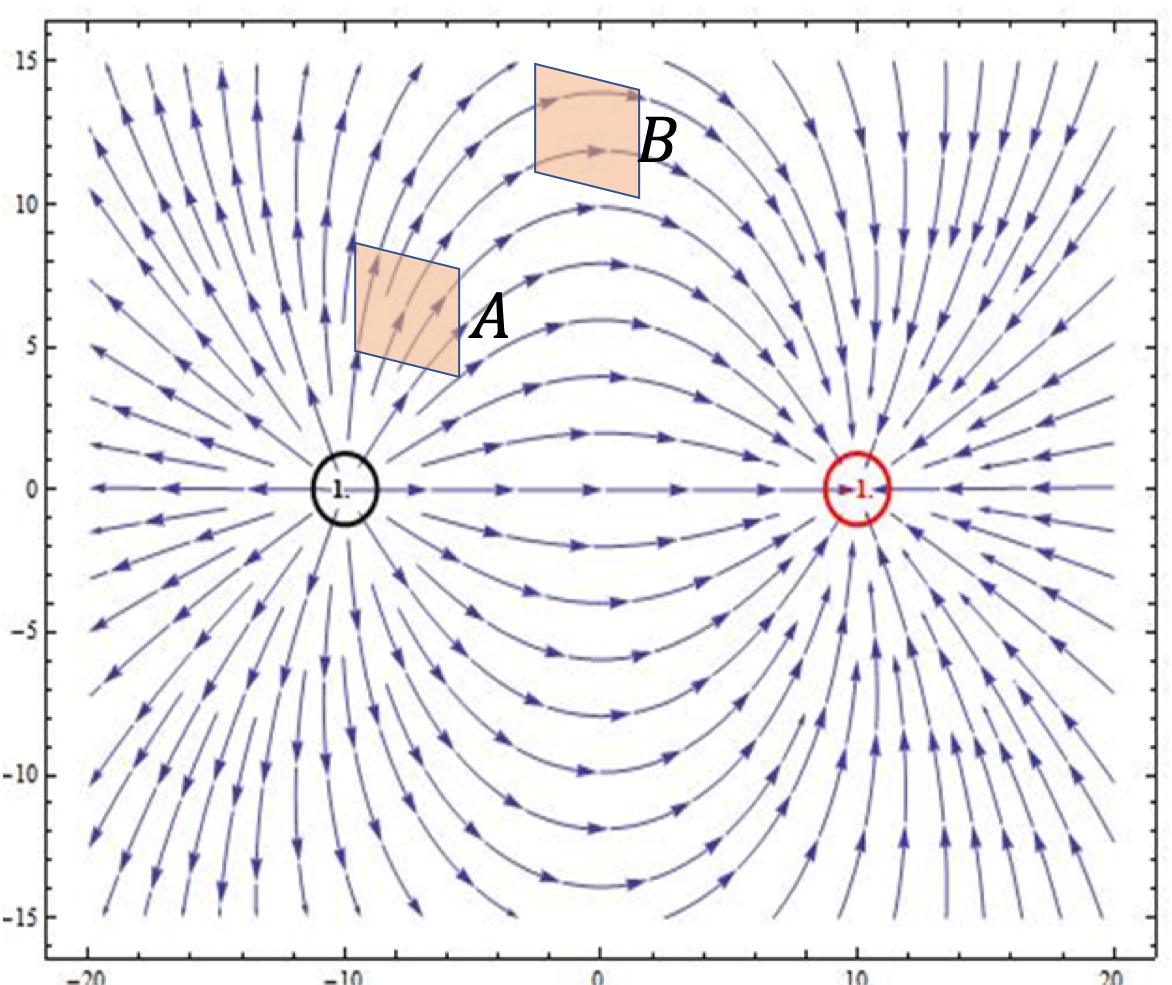
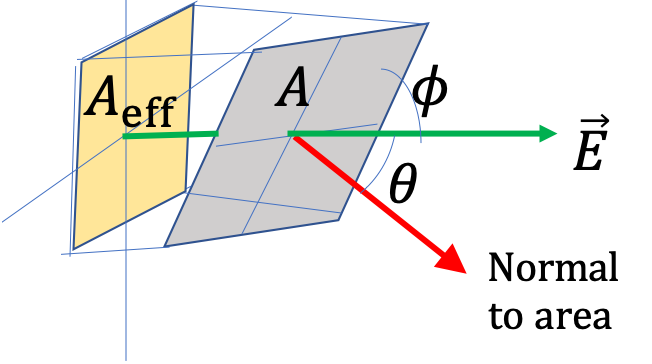
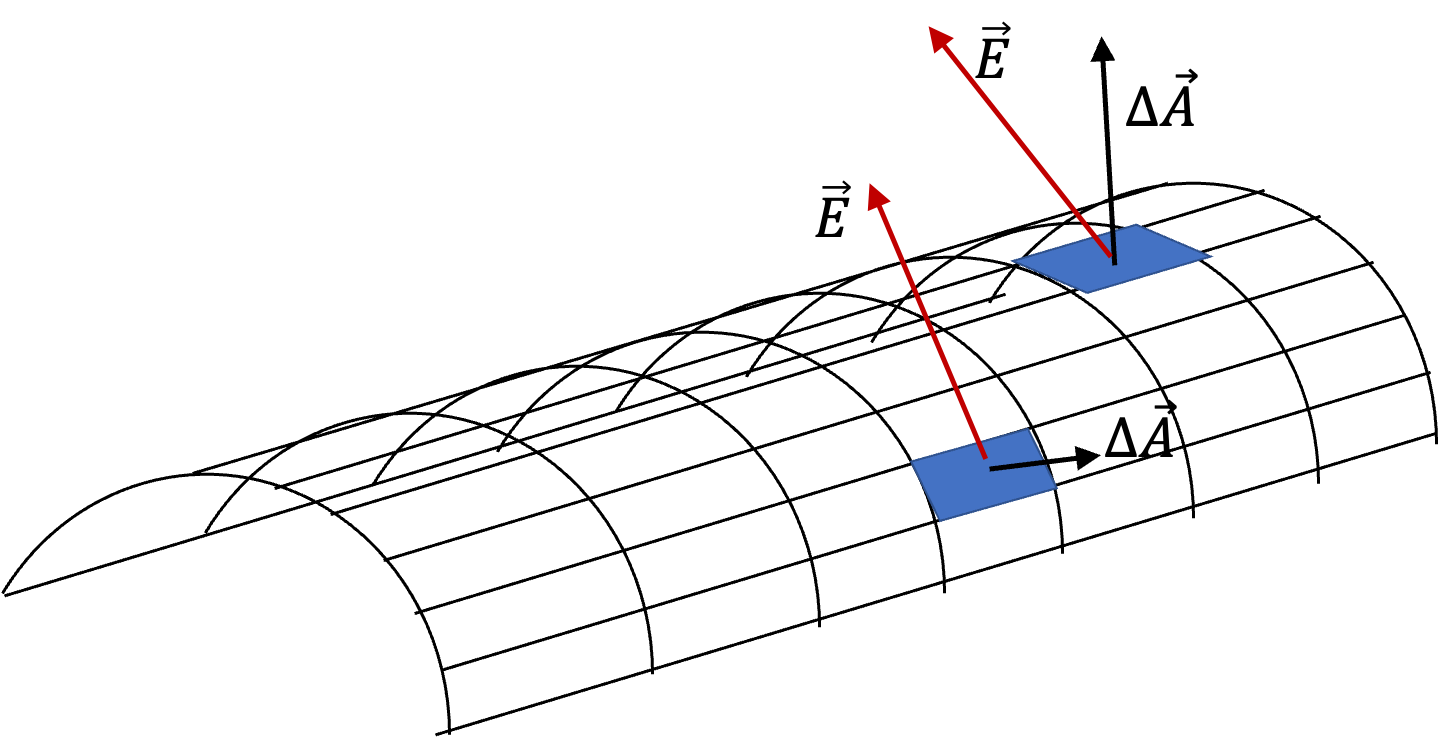
Example 30.6. Electric Flux of Constant Electric Field for Various Orientation of the Area.

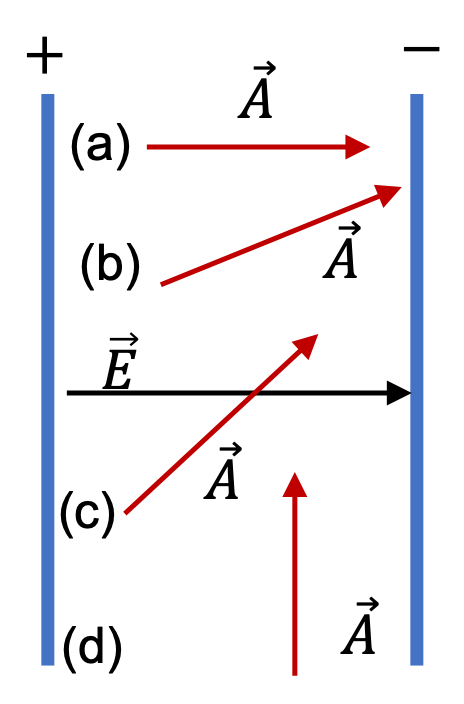
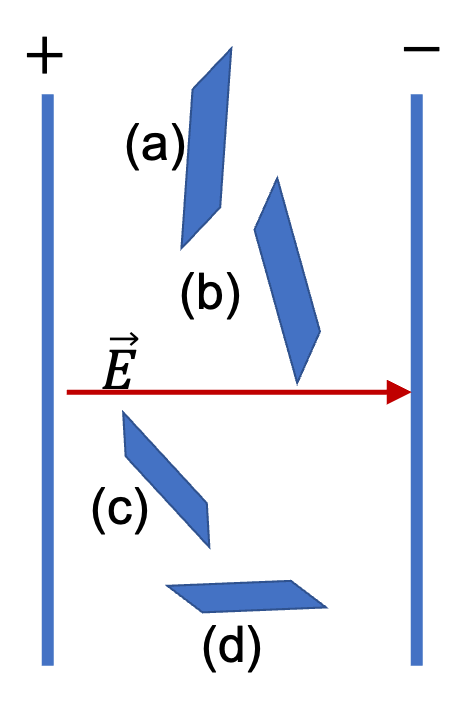
There exists a constant electric field of magnitude \(10,000\text{ N/C}\) between two oppositely charged metal plates, which are parallel to the \(xy\) plane with the negative plate at \(z=0\) and the positive plate at \(z=3\text{ cm}\) .

What will be the electric flux through a rectangle of area \(1.5\text{ cm}^2\) between the plates if the normal to the area makes following angles with respect to the \(z\) axis: (a) \(0^\circ\text{,}\) (b) \(30^\circ\text{,}\) (c) \(60^\circ\text{,}\) (d) \(90^\circ\text{?}\)

Answer.

(a) \(1.5\text{ N.m}^2\text{/C}\text{,}\) (b) \(1.3\text{ N.m}^2\text{/C}\text{,}\) (c) \(0.75\text{ N.m}^2\text{/C}\text{,}\) (d) \(0\text{.}\)

Solution.

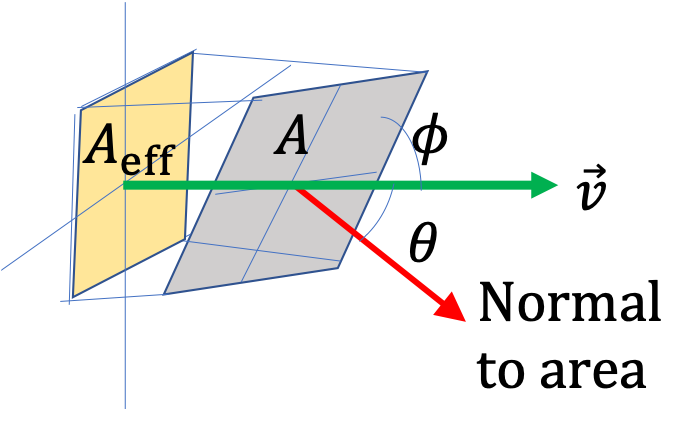
The figure shows the normal vectors to the areas in the four parts. The given angle is the angle \(\theta\text{.}\) Therefore, the flux will be given by

\begin{equation*} \Phi_E = E\,A\,\cos\,\theta. \end{equation*}

Therefore, we get the following values.

\begin{align*} \amp (a) 10,000\times 1.5\times 1 = 1.5\text{ N.m}^2\text{/C}.\\ \amp (b) 10,000\times 1.5 \times \cos\,30^{\circ} = 1.3\text{ N.m}^2\text{/C}.\\ \amp (c) 10,000\times 1.5 \times \cos\,60^{\circ} = 0.75\text{ N.m}^2\text{/C}.\\ \amp (d) 10,000\times 1.5\times \cos\,90^{\circ} = 0. \end{align*}

Example 30.9. (Calculus) Electric Flux of a Point Charge Through a Spherical Surface.

The electric field of a point charge \(q\) at origin is

\begin{equation*} \vec E = \dfrac{1}{4\pi\epsilon_0}\, \dfrac{q}{r^2}\,\hat u_r, \end{equation*}

where \(\hat u_r\) is a radially outward unit vector. What is the electric flux of this electric field through a spherical surface of radius \(r=a\) with center at the origin?

Answer.

\(q/\epsilon_0\text{.}\)

Solution.

The area element at the surface of radius \(r=a\) will be

\begin{equation*} d\vec A = a^2\sin\,\theta\,d\theta\,d\phi\, \hat u_r. \end{equation*}

The electric field at the location of the area element is obtained by setting \(r=a\) in the expression for electric field given.

\begin{equation*} \vec E = \dfrac{1}{4\pi\epsilon_0}\, \dfrac{q}{a^2}\,\hat u_r. \end{equation*}

Taking the dot product of electric field and the area element cancels out the radius \(a\) and get rids of the unit vectors, giving us

\begin{equation*} \vec E \cdot d\vec A = \dfrac{q}{4\pi\epsilon_0}\, \sin\,\theta\,d\theta\,d\phi \end{equation*}

We need to integrate this over the two variables, over the ranges, \(0\le\theta\lt\pi\) and \(0\le\phi\lt 2\pi\text{.}\) They yield the solid angle \(4\pi\text{,}\) which cancels \(4\pi\) the in the denominator. Therefore,

\begin{equation*} \Phi_E = \dfrac{q}{\epsilon_0}. \end{equation*}

Example 30.10. Electric Flux Through a Disk Above a Point Charge.

Find the electric field of the point charge through a circular area of radius \(\sqrt{R^2 - h^2}\) a distance \(h\) away from the charge and oriented such that surface of the area is perpendicular to the line joining the charge and the center of the area.

Answer.

\(\dfrac{q}{2 \epsilon_0} \left( 1 - \dfrac{h}{R}\right).\)

Solution.

In Figure 30.12 we notice that all the field lines that pass through area \(A\) of the disk also pass through the area of the spherical cap \(A_\text{cap}\text{.}\) So, the flux through \(A\) will equal flux through \(A_\text{cap}\text{.}\)

\begin{equation*} \Phi_{\text{through }A} = \Phi_{\text{through }A_\text{cap}}. \end{equation*}

Figure 30.12. Flux through \(A\) is same as the flux through \(A_\text{cap}\) since every field line that passes through \(A\) must also pass through \(A_\text{cap}\text{.}\) The advantages of using \(A_\text{cap}\) explained below.

One advantage of using the cap to find the flux is that vector area elements \(d\vec{A}_\text{cap}\) of the cap and \(\vec E\) are both radial at all points of the cap. This will make the dot product for flux easy. One other advantage is the electric field has the same magnitude at all points of the cap. Therefore, flux will simply be this magnitude times area of the cap, as was the case for the spherical surface around point charge in Example 30.9.

\begin{equation*} \Phi_E = E_\text{at cap} \times A_\text{cap}, \end{equation*}

with

\begin{equation*} E_\text{at cap} = \dfrac{1}{4\pi \epsilon_0}\,\dfrac{q}{R^2}. \end{equation*}

This reduces the problem to the problem of computing the area of the cap. This will be

\begin{equation*} A_\text{cap} = R^2\times \Omega, \end{equation*}

where \(\Omega\) is the solid angle subtended by the cap. Placing the ring perpendicular to the \(z\) axis as in Figure 30.12 helps with this calculation. The cap has maximum angle from the \(z\) axis to be

\begin{equation*} \theta_\text{max} = \cos^{-1}\left(\dfrac{h}{R} \right). \end{equation*}

If you do not have a Calculus background, you can look up a formula for the solid angle of a cap given this \(\theta_\text{max}\text{:}\)

\begin{equation*} \Omega = 2\pi\left( 1 - \dfrac{h}{R}\right). \end{equation*}

You can see that the angle of the full cap will be when \(h=-R\text{.}\) In that case, you get \(4\pi\text{.}\) However, if you have Calculus background, you can prove this result by integrating over the two spherical angles.

\begin{align*} \Omega \amp = \int_0^{2\pi} d\phi \int_0^{\theta_\text{max}}\,\sin\,\theta\, d\theta,\\ \amp = 2\pi \left( 1 - \dfrac{h}{R}\right). \end{align*}

In any case, using the solid angle we get the area of the spherical cap, and get the flux.

\begin{align*} \Phi_E \amp = \dfrac{1}{4\pi \epsilon_0}\,\dfrac{q}{R^2} \times R^2\times 2\pi \left( 1 - \dfrac{h}{R}\right), \\ \amp = \dfrac{q}{2 \epsilon_0} \left( 1 - \dfrac{h}{R}\right). \end{align*}

Prev Top Next