Photoelectric effect demonstrated that energy in light came in bunches or quanta called photons. If photons really do exist as particles, each photon would have energy as well as momentum. We have seen that the energy of a photon is equal to \(hf\text{.}\) Since a photon must travel at the speed of light, its rest mass must be zero as shown in the chapter on relativity. This gives the following expression for the momentum of a photon.
\begin{equation}
p = \dfrac{E}{c} = \dfrac{h f}{c} = \dfrac{h}{\lambda},\tag{50.21}
\end{equation}
where I have replaced \(f/c = \lambda\text{,}\) where \(\lambda\) is the wavelength of the electromagnetic wave. We will often refer to \(f\) and \(\lambda\) the frequency and wavelength of the photon, even though they refer to the frequency and wavelength of the electromagnetic wave that the photon belongs to.
Arthur Compton of Washington University in St. Louis, Missouri analyzed the energy and momentum conservation in the process of collision of a photon with an electron and found that, the photon coming at an angle to the original direction after collision will have a different wavelength than the wavelength of the incident photon. The predicted shift in wavelength was small, of the order of picometers, and was independent of the wavelength of the incoming photon. Since X-rays have wavelengths in the picometer range the experiment is usually done with X-rays as Compton had done. Also, since the work function of a surface is in the electron-volt (eV) range while the energy of a photon in X-ray has energy in the keV range, we ignore the work function completely.
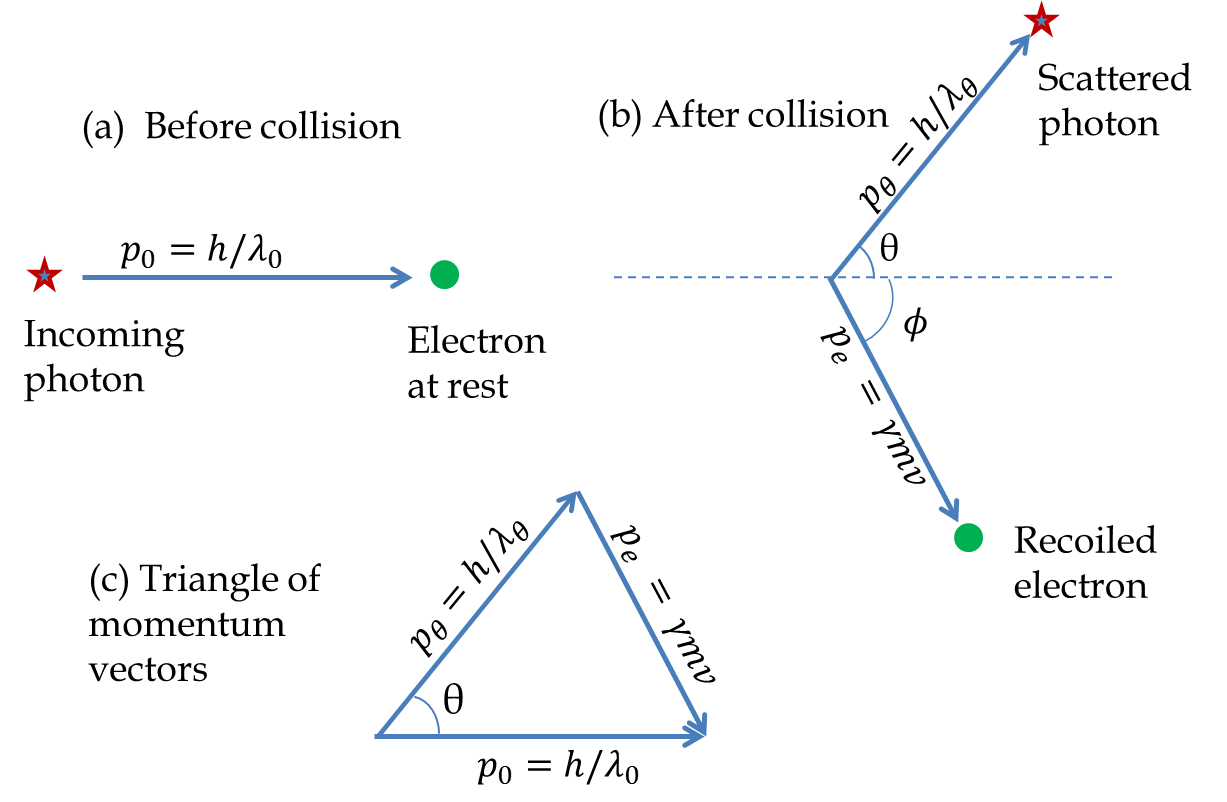
Let \(\vec p_0\) be the momentum of the incoming photon, \(\vec p_\theta\) the momentum of the outgoing photon at angle \(\theta\text{,}\) and \(\vec p_e\) be the momentum of the recoiled electron. The vector equation of conservation of momentum will be
\begin{equation}
\vec p_0 = \vec p_{\theta} + \vec p_e.\tag{50.22}
\end{equation}
These vectors form a triangle as shown in
Figure 50.33. The law of cosine applied to the triangle gives the following relation between the magnitudes of the momenta and angle
\(\theta\text{.}\)
\begin{equation}
p_e^2 = p_0^2 + p_{\theta}^{2} + 2 p_0 p_{\theta}\cos\theta,\tag{50.23}
\end{equation}
with the momenta given by the following:
\begin{equation}
p_0 = \frac{h}{\lambda_0}\ ,\quad p_{\theta} = \frac{h}{\lambda_{\theta}}\ ,\quad p_e = \gamma m v\ ,\quad \gamma = \frac{1}{\sqrt{1-v^2/c^2}},\tag{50.24}
\end{equation}
where \(v\) is the speed of the recoiled electron, \(\lambda_0\) is the wavelength of the incoming photon, and \(\lambda_\theta\) the wavelength of the outgoing photon at angle \(\theta\text{.}\) Therefore, we get the following equation from the conservation of momentum
\begin{equation}
\frac{m^2 v^2}{1-v^2/c^2} = \left(\frac{h}{\lambda_0}\right)^2 + \left(\frac{h}{\lambda_{\theta}}\right)^2 -2 \frac{h^2}{\lambda_0\lambda_{\theta}}\cos\theta. \tag{50.25}
\end{equation}
The conservation of energy will give
\begin{equation}
\frac{hc}{\lambda_0} + mc^2 = \frac{hc}{\lambda_{\theta}} + \frac{mc^2}{\sqrt{1-v^2/c^2}}.\tag{50.26}
\end{equation}
Since the velocity of the recoiled electron is not measured in the experiment we will eliminate
\(v\) from Eqs.
(50.25) and
(50.26). A long and tedious calculation gives the following result.
\begin{equation}
\lambda_{\theta} - \lambda_0 = \frac{h}{mc} ( 1 - \cos\theta). \tag{50.27}
\end{equation}
The quantity \(\Delta\lambda = \lambda_{\theta} - \lambda_0\) is called the Compton shift and the quantity \(\lambda_c = \dfrac{h}{mc}\) is called the Compton wavelength of the particle of mass \(m\text{,}\) which is the mass of electron here. Putting the value of \(h\text{,}\) \(c\text{,}\) and \(m\) in \(\dfrac{h}{mc}\) we find the Compton wavelength of an electron to be
\begin{align*}
\lambda_c \amp = \frac{h}{mc} = \frac{6.63\times 10^{-34}\textrm{J.s}}{9.11\times 10^{-31}\textrm{kg} \times 3.0\times 10^{8}\textrm{m}}\\
\amp = 2.43\times 10^{-12}\:\textrm{m} = 2.43\: \textrm{pm}.
\end{align*}
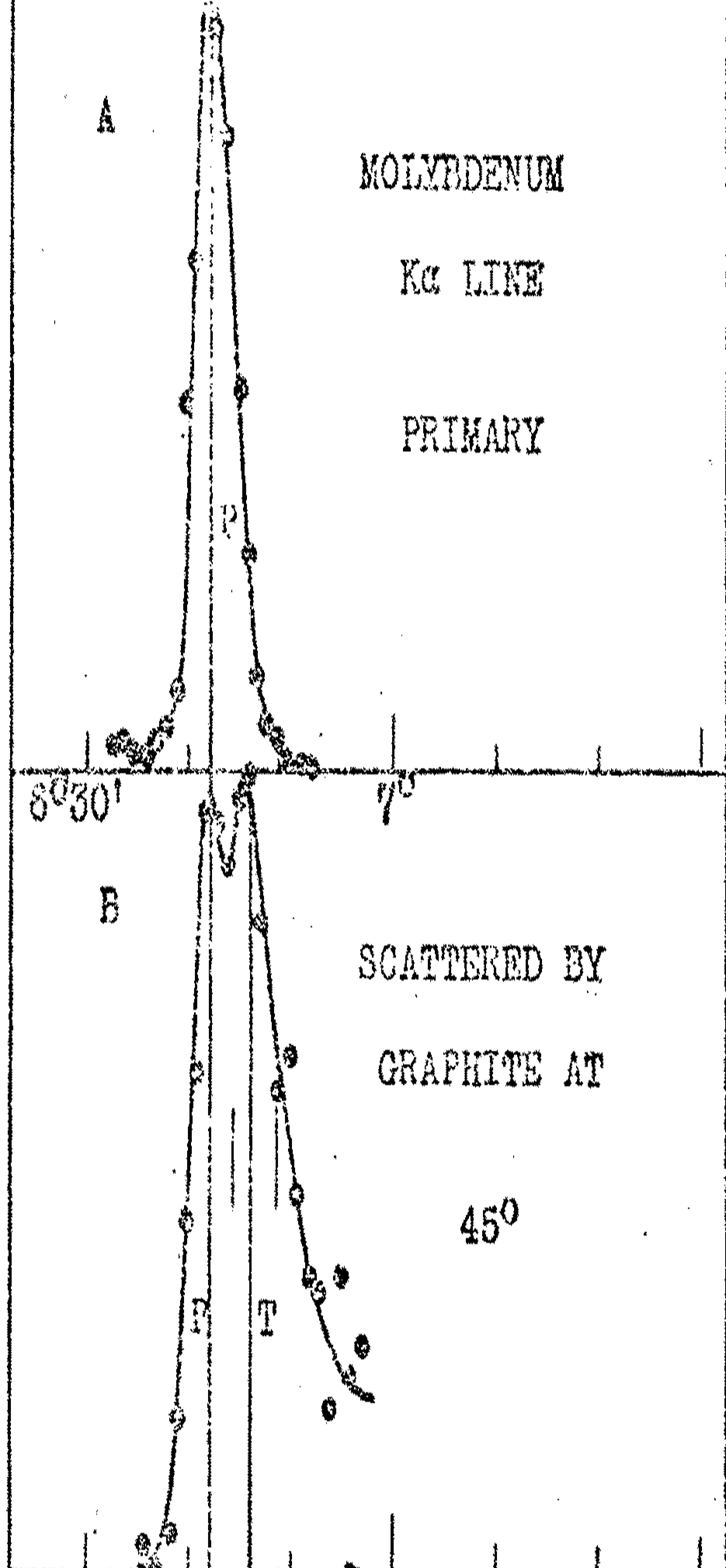
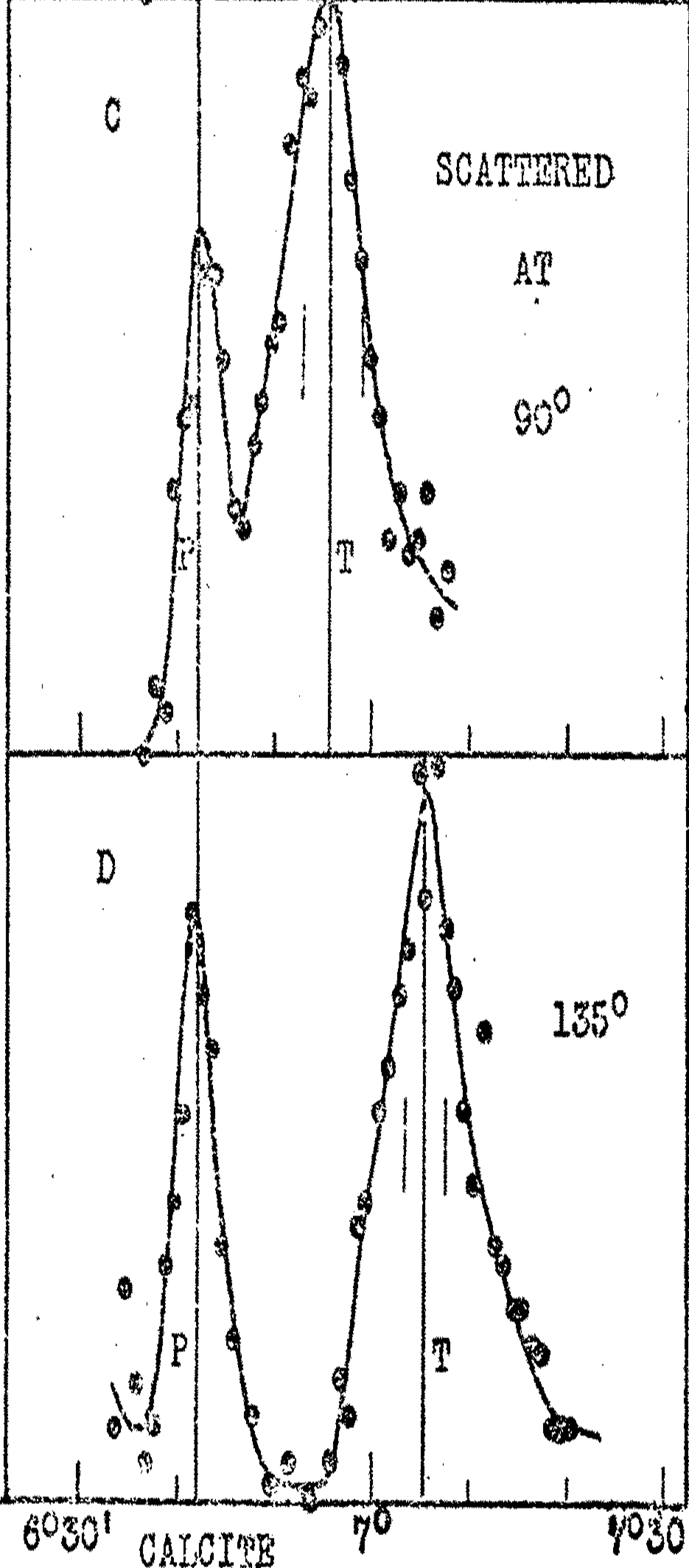
According to Equation
(50.27) no shift will be seen in the forward direction,
\(\theta = 0\) and a maximum shift will occur at the back scattered direction,
\(\theta = 180^{\circ}\text{.}\) At
\(90^{\circ}\) the shift will equal the Compton wavelength of the object that the photon was scattered from.