First Law of Thermodynamics

Section 24.1 First Law of Thermodynamics

Subsection 24.1.1 Energy Change of a Thermally Insualted System

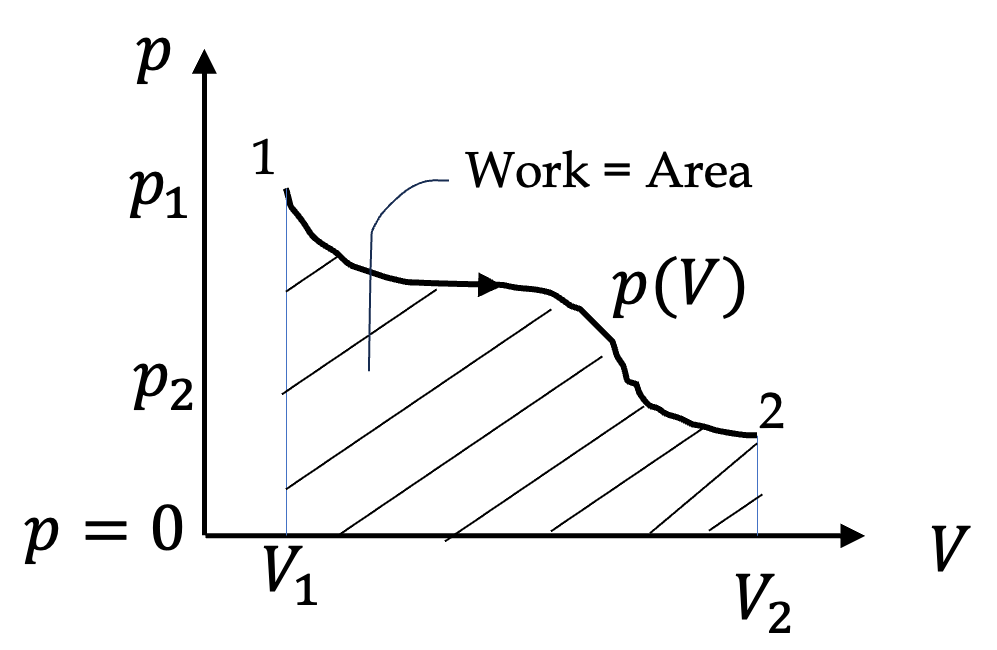
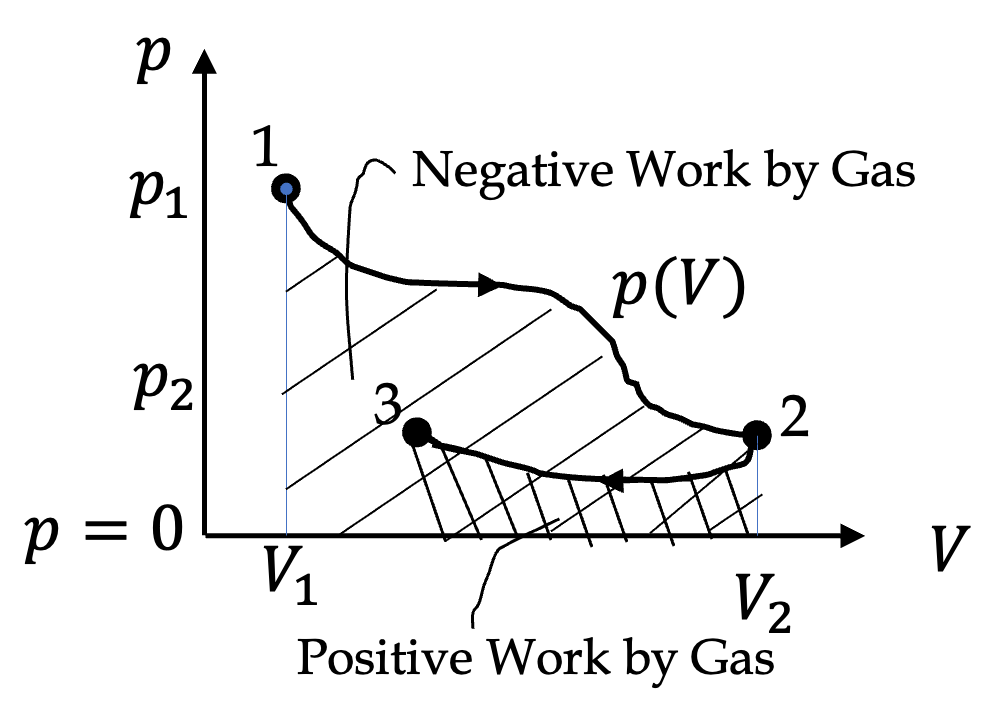
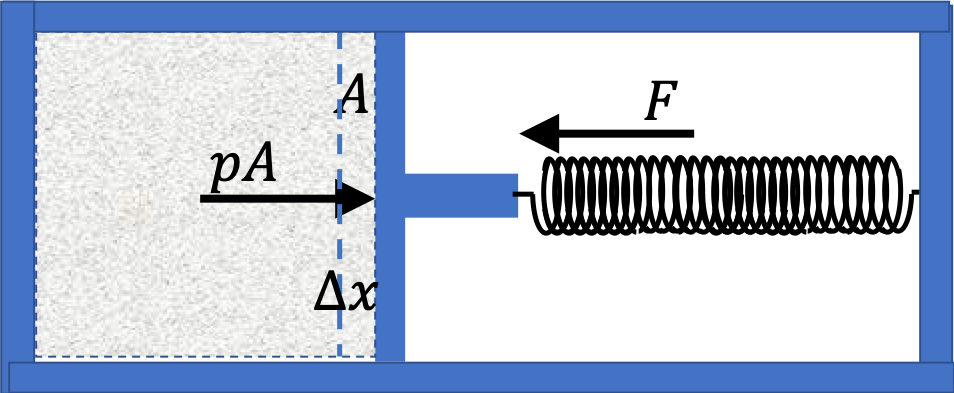
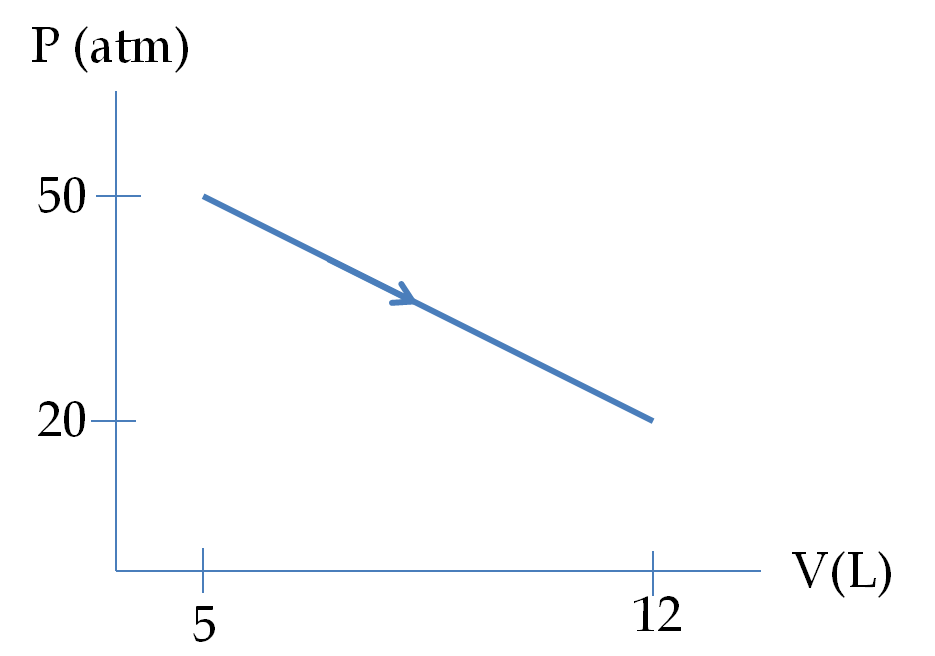
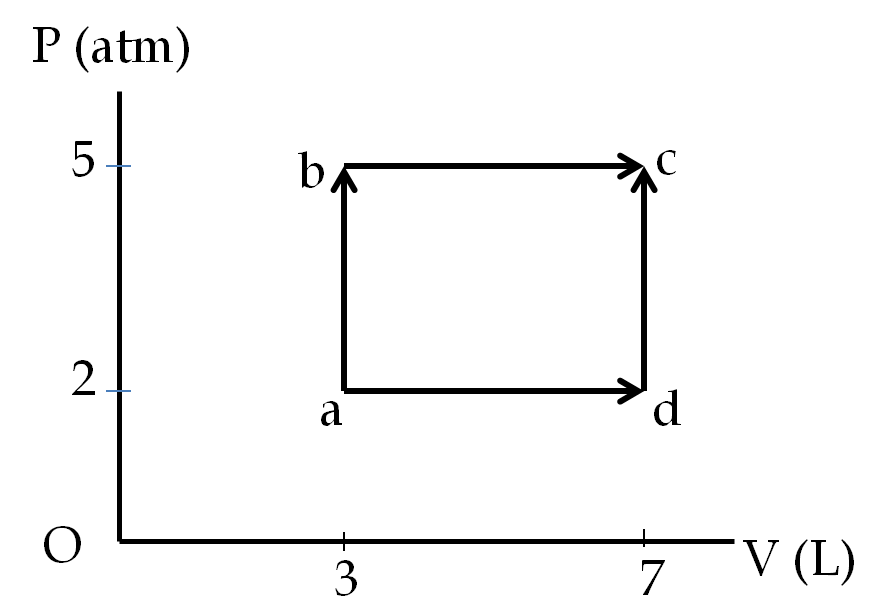
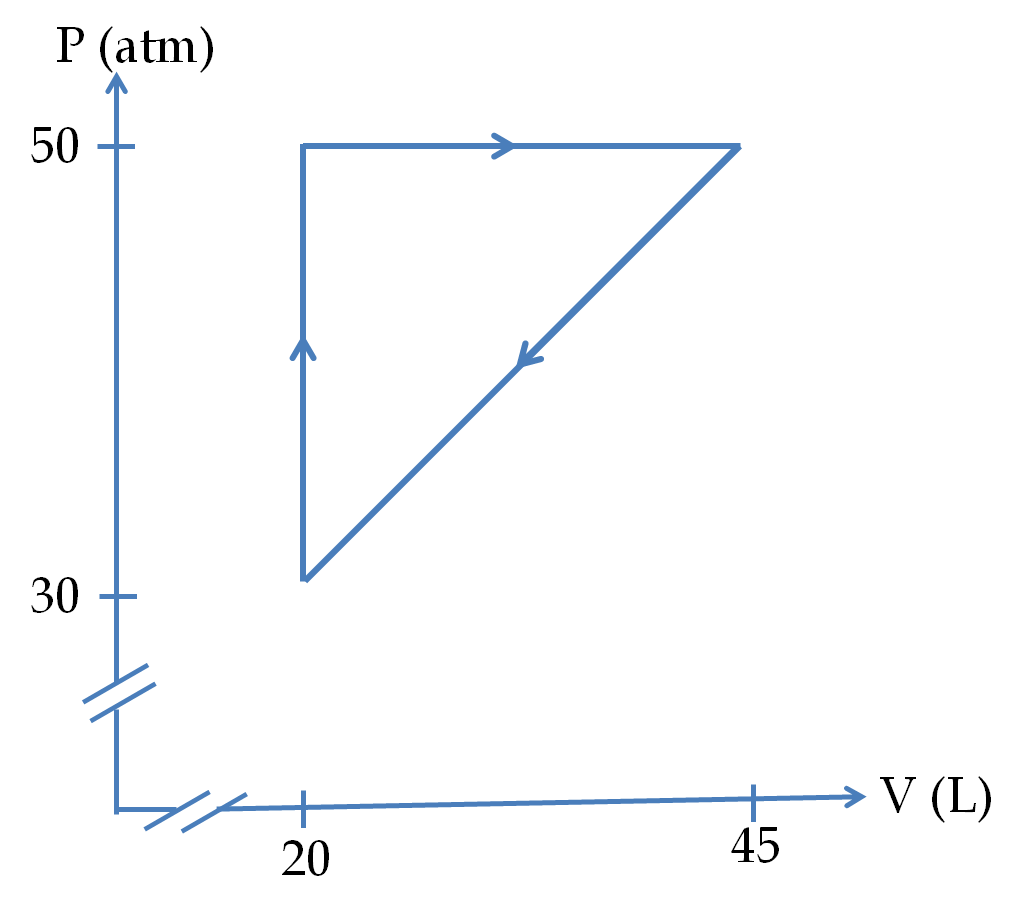
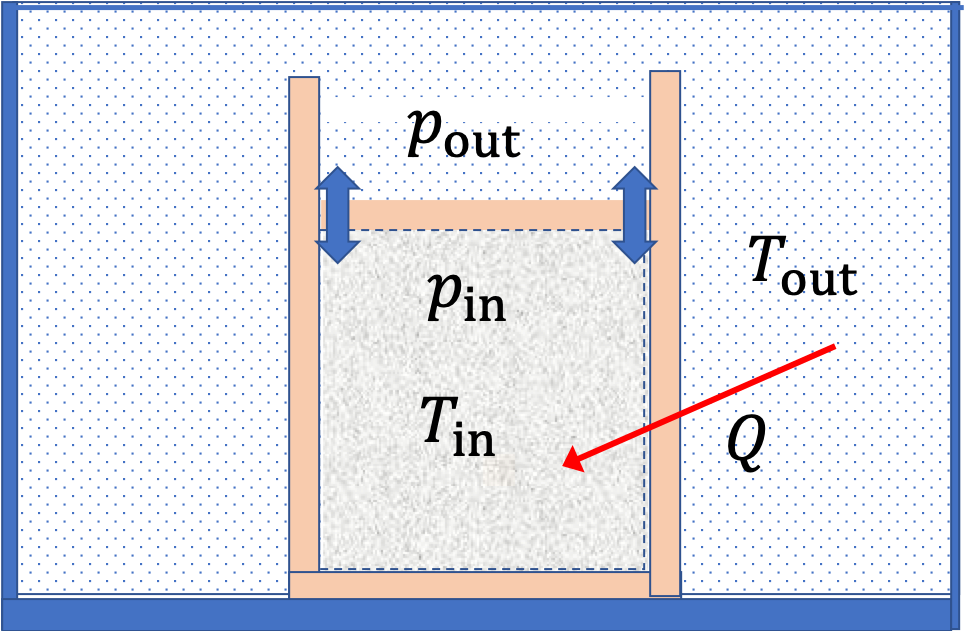
To get oriented with the energy considerations in a thermodynamic system, let us consider a simple system of a gas contained in a cylinder with movable piston as in Figure 24.1. Suppose the cylinder and piston are thermally insulated from the environment.

Figure 24.1. The gas on the left side expands and contracts in a thermally insulated environment. The piston of the gas-contaning part is moved by compression and extension of a spring. In the part of the cycle in which spring is extending from compressed to natural length or spring is shrinking towards natural length from an extended state, energy in the spring flows into the gas. In other parts of the cycle, energy flows from gas to the spring.

Let us examine a process in which gas is being compressed. Suppose the force on the piston by the spring is infinitesimally larger than the force by the gas so that the piston moves by a distance \(\Delta x \lt 0\) into the gas, corresponding to change in volume \(\Delta V \lt 0\text{.}\) The work done by the spring force will be

\begin{equation*} W_\text{by spring on gas} = -F\Delta x \gt 0. \end{equation*}

During this time \(F \approx pA\) and \(\Delta V = A\Delta x\text{.}\) Thus, we can rewrite the work in state properties of the gas.

\begin{equation*} W_\text{by spring on gas} = -p\Delta V \gt 0. \end{equation*}

The work by the gas will be opposite of this and so will have opposite sign.

\begin{equation} W_\text{by gas} = p\Delta V\ \lt 0.\tag{24.1} \end{equation}

In the gas compression, we find that work by the gas is negative but the energy of the gas goes up since energy flows from the spring to the gas. Thus, we state the change in energy of the gas (our system) by the following equation.

\begin{equation*} \Delta E_\text{of gas} = -W_\text{by gas} = -p \Delta V. \end{equation*}

Let us drop the subscript “by gas” and write this for an infinitesimal process.

\begin{equation} dE = -pdV.\ \ \ \text{(thermally insulated system)}\tag{24.2} \end{equation}

The negative sign also work for the process in which gas is expanding, thus reducing its energy by the work by the gas will be positive. Here, we see the exchange of energy occur through the performance of a mechanical work. Next we will see another mechanism of exchange of energy.

Remark 24.2. Work by System in a Finite Process.

Eq. (24.2) gives us a formula for work by the system in an infinitesimal process.

\begin{equation*} dW = -pdV. \end{equation*}

What will be work over a finite process, say of a gas whose thermodynamic state goes from \((p_1, V_1, T_1)\) to \((p_2, V_2, T_2)\) through a process over which pressure is given as a function of volume, i.e., path is some function \(p(V)\) or both pressure and volume at each point are given in terms of temperature \(T\) or some parameter.

\begin{equation} W_{12} = -\int_\text{process}\, p dV.\tag{24.3} \end{equation}

Often, a process is given in the \((p,V)\) plane of the system. In that case, the process is a directed path as showin in Figure 24.3. The area under each expansion or contraction gives work for that expansion or contraction with a negative sign for the expansion and positive sign for the contraction part. Figure 24.3 corresponds to an expansion, hence the work will be negative.

If a process has both expansion and contraction parts, these individual component works are then added algebraically to get the net work for the entire process. In Figure 24.4, the entire process 1-2-3 will have negative area under 1-to-2 and positive area under 2-to-3. The work for 1-2-3 process will be an algebraic sum of \(W_{12}\) and \(W_{23}\text{,}\) which would be a negative in this figure.

Example 24.5. Work Done in a Constant Pressure Process.

A gas cylinder with movable piston contains \(10\) moles of a gas. The gas expands under a constant pressure of \(24\) atm from \(10\) liters to \(12\) liters. (a) Find the work done by-the-gas in \(\text{L.atm}\text{.}\) (b) Express your answer in \(\text{J}\text{.}\)

Answer.

(a) \(-48\,\text{L.atm}\text{,}\) (b) \(-4,864\,\text{J}\text{.}\)

Solution.

Since pressure is constant during the process, \(p\) can come outside the integral gicving the following results.

\begin{equation*} W_{12} = -\int_\text{process}\, p d V = - p \int_{V_1}^{V_2} dV = -p(V_2 - v_1) = - 24\times (12 - 10) = -48\,\text{L.atm}. \end{equation*}

We can convert the unit of work from \(\text{L.atm}\) to \(\text{J}\) by

\begin{equation*} 1\, \text{L.atm} = 101.325\,\text{J}. \end{equation*}

Thus, we get the answer in Joule to be \(-4,864\,\text{J}\text{.}\)

Example 24.6. Work Done by an Ideal Gas in a Constant Temperature Process.

A gas cylinder with a movable piston contains \(n\) moles of an ideal gas in state \((p_1, V_1, T_1)\text{.}\) The gas expands by moving the piston slowly in a process where temperature is maintaind at \(T_1\) to a final state of the gas \((p_2, V_2, T_1)\text{.}\) What is the work done by-the-gas?

Answer.

\(-nRT_1\ln\frac{V_2}{V_1}\text{.}\)

Solution.

Since the gas is an ideal gas, at every point in the process it will abide by the the ideal gas law

\begin{equation*} pV = n R T, \end{equation*}

so that we will have \(p\) in terms of \(V\) at every point of the process. With \(T=T_1\) we have

\begin{equation*} p = \frac{nRT_1}{V}. \end{equation*}

Using this in the formula for work and taking the constant outside the integral we get

\begin{equation*} W = -\int\,p\,dV = -nRT_1\int_{V_1}^{V_2}\,dV = = -nRT_1\ln\frac{V_2}{V_1}. \end{equation*}

Here, we can replace \(nRT_1\) by \(p_1V_1\) since \(p_1V_1 = n RT_1\text{.}\)

Example 24.7. Expansion into a Vacuum.

Some ideal gas is placed into a container of volume \(V\) that has a lid that can be opened remotely. The container is then placed into a very large chamber which is evacuatted to a “perfect vacuum”. The lid is then openned to the vacuum which makes the gas expand essentially against vacuum. How much work is done by the gas?

Solution.

Since gas expands without any opposing force, it does not do any work. If the gas was not an ideal gas, the gas will need to do work against the cohesive intermolecular force. But, there are no intermolecular forces in an ideal gas, therefore, work done would be zero.

Subsection 24.1.2 Energy Change for a Fixed-Volume System

In the above we saw how energy of a thermally insulated system can change by way of work. Let us now consider a situation as illustrated in Figure 24.8, where the system is in thermal contact with the outside world but it cannot do any work due to its volume not allowed to change by placing it in a rigid container. The container now is made up of a good heat conductor. Of course, we intend to ignore any volume change of the container.

Figure 24.8. The gas is heated by heating water in the bath and energy \(Q \) flows into the gas through the thermally conductive walls. The volume of the gas is kept fixed by stoppers on the piston so that gas does’t do any work.

Suppose the gas is initially at temperature \(T\) and in thermal equilibrium with a water bath also at temperature \(T\text{.}\) When you heat water bath, its temperature will increase. You will find that energy begins to flow into the gas raising its temperature as well. But since the volume of the gas did not change, the energy change of the gas is not by a mechanical work, but by some other mechanism - a mechanism that requires a difference in temperarture across a thermally conductive material. This mechanism of energy transfer is what we have called heat transfer.

If you look at the heating process microscopically, you find that, as temperature of water rises, the water molecules move faster, and when they collide with the container, they transfer some of the energy and momentum to the container molecules, which in turn transfer energy to the gas molecules inside. The energy transfer by heat is the collective work of a large number of molecules.

We denote energy exchange by the mechanism of heat by letter \(Q\) or \(Q_\text{if}\text{,}\) where the subscript refers to the initial-to-final process, or \(Q_\text{into}\text{,}\) where “into” is for energy entering into the system. Often \(Q \) is called heat energy, but it is not like kinetic energy or potential energy, but rather an energy involving very kinetic and potential energies of large number of molecules, both within the molecules and in-between the molecules. The sign convention is chosen to coincide with change in energy. That is, change in energy positive for positive \(Q\text{.}\)

\begin{equation*} \Delta E_\text{of gas} = Q_\text{into gas}. \end{equation*}

Once again, we can state this observation as a conservation of energy statment. Think of the gas as the thermodynamic system and the water bath as the environment, then we have

\begin{equation*} \Delta E_\text{of gas} = Q_\text{into gas} = - \Delta E_\text{of environment} \end{equation*}

Remark 24.9. Using Specific Heat and Heat of Transfrmation for Computing Heat.

Recall that we can quantify heat involved by monitoring temperature change and/or phase transformation as a result of heating or cooling a system. The formulas for heat associated with an infinitesimal temperature change \(dT\) of a system containing mass \(m\) of a substance of specific heat \(c\) is given by

\begin{equation} dq = m\,c\, dT,\tag{24.4} \end{equation}

and for transformation of an infinitesimal mass \(dm\) of a substance of heat of transformation \(l\) is

\begin{equation*} dq = l\, dm. \end{equation*}

The calculations for a finite process gets complicated since \(c\) often depends on how the heating or cooling is done, e.g., if the heating or cooling is done by keeping pressure unchanged, then we need to use specific heat at constant pressure \(c_p\text{,}\) and if the heating or cooling is done by keeping the volume unchanged, then we need to use specific heat at constant volume \(c_V\text{.}\) Further complicating factor is that specific heat \(c\) depends on temerature. Hence, when we integrate Eq. (24.4), we cannot just pull out \(c\text{,}\) instead, we must integrate over the function \(c(T)\text{.}\) Hence, for finite temperature chage from, say \(T_1\) to \(T_2\) we will write

\begin{equation} Q_{12} = m\, \int_{T_1}^{T_2}\, c(T)\, dT.\tag{24.5} \end{equation}

Example 24.10. Heat Flow in Heating Liquid Water.

Two kg of liquid water in a beaker is heated from \(20^\circ\text{C}\text{,}\) to \(95^\circ\text{C}\) at constant pressure with water remaining in the liquid state. In this range of temperature, specific heat of water is independent of temperature and has the constant value \(4,184\,\text{J}.\text{kg}^{-1}.\,^\circ\text{C}^{-1}\text{.}\) How much heat has flown into-the-water?

Solution.

Since specific heat here is independent of temperature, the integration just becomes product, giving

\begin{equation*} Q_{12} = + 2\,\text{kg} \times 4,184\,\text{J}.\text{kg}^{-1}.\,^\circ\text{C}^{-1} \times \left(95 - 20 \right) = 627,600\,\text{J}. \end{equation*}

These are large numbers. That’s because the unit we are using. Let’s convert it to calories. There are \(1\,\text{cal} = 4,184\,\text{J}\text{.}\)

\begin{equation*} Q_{12} = \frac{627,600}{4184} = 150\,\text{cal}. \end{equation*}

Example 24.11. Heat Flow into a Copper Block While Melting the Block.

Twenty kilograms of copper is melted at its melting point of \(1,085^\circ\text{C}\text{.}\) How much heat flows into that copper block? The heat of melting of copper = \(206\,\text{kJ/kg}\text{.}\)

Solution.

It is just an illustration of the use of heat of transformation. Let state 1 be solid copper at \(1,085^\circ\text{C}\) and state 2 be liquid copper \(1,085^\circ\text{C}\)

\begin{equation*} Q_{12} = m l = 20\,\text{kg} \times 206\,\text{kJ/kg} = 4120\,\text{kJ}. \end{equation*}

Subsection 24.1.3 First Law of Thermodynamics

In the last two subsections, we identified two mechanisms by which energy of a thermodynamic system can change - (1) energy flow due to work \(W\) and (2) energy flow \(Q\) due to a temperature difference across a thermal contact. Summing these two mechanisms gives us the statement of First Law of Thermodynamics. In Physics, we write the change in energy of the system in terms of work-by-the-system and heat-into-the-system with appropriate signs for consistency.

\begin{equation} \Delta E_\text{of system} = Q_\text{into system} - W_\text{by system}.\tag{24.6} \end{equation}

Notice that we need to be careful with the signs: \(Q\) is positive if system heats up and negative if system cools, and \(W\) is positive if system expands and negative if system contracts.

Subsection 24.1.4 First Law of Thermodynamics and Internal Energy

Often in thermodynamics, we study energy changing processes that do not involve changing the translational kinetic energy or rotational kinetic energy or the gravitational potential energy or other forms of potential energy associated with the entire body.

The energy of the system that does change during a thermal process are all concerned with the molecular motion, whether it be the kinetic energy of molecules or vibrational energy of atoms bound to molecules or rotational energy of molecules or intermolecular interactions, etc. The net of these internal sources of energy is called internal energy of the system. The internal energy is usually denoted by the symbol \(U\text{.}\) Thus change in energy in a thermal process will be

\begin{equation*} \Delta E_\text{system} = \Delta U_\text{system}.\ \ \ \text{(thermal process)} \end{equation*}

In terms of internal energy, the first law of thermodynamics for the change in the energy of the system will be

\begin{equation} \Delta U = Q - W,\tag{24.7} \end{equation}

where I have dropped all the subscripts. As always, \(U\) is of-the-system, \(Q\) is into-the-system, and \(W\) is by-the-system. Make sure you understand the sign convention used in this frmulation. For your conveniece, I will summarize the rules for sign convetion here.

Sign Conventions:

Heat entering into the system: \(Q \gt 0 \text{.}\)
Heat leaving into the system: \(Q \lt 0 \text{.}\)
The system loses energy: \(W \gt 0 \text{.}\)
The system gains energy: \(W \lt 0 \text{.}\)

Example 24.12. Work, Heat, and Internal Energy in a Thermal Expansion of Steam.

Consider the process for steam in a cylinder shown in Figure 24.13. Suppose the change in the internal energy in this process is 30 kJ. Find the heat entering the system.

Answer.

\(61,900\ \text{J}\text{.}\)

Solution.

The work by the system in the given process is

\begin{equation*} W_{ab} = \text{Area under the curve to the } p = 0 \text{ line.} \end{equation*}

This gives the sum of the area of a triangle and a rectangle.

\begin{align*} W_{ab} \amp = \left(\frac{1}{2} \times 9\ \text{L}\times 30\ \text{atm} + 9\ \text{L}\times 20\ \text{atm}\right) \times \frac{101.3\text{ J}}{\text{L.atm}}\\ \amp = 31,910\ \text{J}. \end{align*}

Therefore

\begin{equation*} U_{ab} = Q_{ab} + W_{ab}\ \ \Longrightarrow\ \ Q_{ab} = 61,900\ \text{J}. \end{equation*}

Example 24.14. Work, Heat and Internal Energy Change in Processes in a Gas.

Consider the processes on a gas shown in Figure 24.15. In the process ab and bc, \(3600\) J and \(2400\) J of heat are added to the system. (a) Find the work done in each of the processes ab, bc, ad and dc. (b) Find the internal energy change in processes ab and bc. (c) Find the internal energy difference between states c and a. (d) Find the total heat added in the adc process. (e) From the information give, can you find heat added in process ad? Why or why not?

Answer.

(a) - 810.4 J, (b) \(\Delta U_{ab}\) = 3600 J, \(\Delta U_{ab}\) = 374 J,(c) 3974 J, (d) 4784 J, and (e) Cannot be determined.

Solution 1. a

\begin{align*} \amp W_{ab} = 0,\\ \amp W_{bc} = 5\ \text{atm}\times 4\ \text{L} \times 101.3\ \frac{\text{J}}{\text{L.atm}} = 2,026\ \text{J},\\ \amp W_{ad} = 2\ \text{atm}\times 4\ \text{L} \times 101.3\ \frac{\text{J}}{\text{L.atm}} = 810.4\ \text{J}, \\ \amp W_{dc} = 0. \end{align*}

Solution 2. b

For the a-b process:

\begin{equation*} \left. \begin{array}{l} W_{ab} = 0\\ Q_{ab} = 3,600\ \text{J} \end{array} \right\} \ \ \ U_{ab} = Q_{ab} - W_{ab} = 3,600\ \text{J}. \end{equation*}

For the b-c process:

\begin{equation*} \left. \begin{array}{l} W_{bc} = 2,026\ \text{J}\\ Q_{bc} = 2,400\ \text{J} \end{array} \right\} \ \ \ U_{bc} = Q_{bc} - W_{bc} = 374\ \text{J}. \end{equation*}

Solution 3. c

\begin{equation*} U_{ac} = U_{ab} + U_{bc} = 3,600 \ \text{J} + 374 \ \text{J}= 3,974\ \text{J}. \end{equation*}

Solution 4. d

\begin{align*} Q_{adc} \amp = U_{ac} + W_{ad} + W_{dc}\\ \amp = 3974 \ \text{J} + 810.4 \ \text{J} + 0 = 4,784.4 \ \text{J}. \end{align*}

Solution 5. e

We cannot determine \(Q_{ad}\) since we do not know \(U_{ad}\) or have a way of determining it. We know only \(W_{ad}\text{.}\) That would give

\begin{equation*} Q_{ad} = U_{ad} + 810.4\ \text{J}. \end{equation*}

Example 24.16. Work, Heat, and Internal Energy in a Cyclic Process.

The state of 30 moles of steam in a cylinder is changed in a cyclic manner from a-b-c-a, where the pressure and volume of the states are a(20 L, 30 atm), b(20 L, 50 atm), and c(45 L, 50 atm), as shown in Figure 24.17. Assume each change takes place along the line connecting the initial and final states in the \(PV\) plane. (a) Find the net work done by the steam in one cycle. (b) Find the net amount of heat flow in the steam over the course of one cycle.

Answer.

(a) \(25,300\ \textrm{J} \text{,}\) (b) \(25,300\ \textrm{J}\text{.}\)

Solution 1. a

The net work will be sum of positive work in bc process and negative work on ca process. This sum equals the area enclosed in the cyclic process, which is just the area of a triangle.

\begin{equation*} W_{abca} = \frac{1}{2} \times 25\ \text{L}\times 20\ \text{atm} = 250\text{ L.atm} \end{equation*}

Converting this to Joules we get

\begin{equation*} W_{abca} = 250\text{ L.atm} \times \frac{101.3\ \textrm{J} }{\textrm{L.atm}} = 25,300\ \textrm{J}. \end{equation*}

Solution 2. b

In a cycle, the state returns to the self. Therefore, the change in internal energy will be zero.

\begin{equation*} U_{abca} = 0. \end{equation*}

Now, we have the inernal energy change and work over one cylce. Therefore, we use the first law of thermodynamics to figure out heat exchanged.

\begin{equation*} Q_{abca} = U_{abca} + W_{abca} = 25,300\ \textrm{J}. \end{equation*}

Subsection 24.1.5 Other Forms of Energy

Yet another approach to energy conservation is based on the various types of energy sources in common vernacular use. For instance, some chemical reactions release energy, we call that energy to be Chemical Energy. Similarly, the energy in a nuclear reaction is called the Nuclear Energy.

Classifying energy into various types is helpful in this regard since an overall energy of each type can often be determined from experiments. The change in internal energy is then written as a sum of

\begin{align*} \Delta U \amp = \Delta E_{\text{chem}} + \Delta E_{\text{nuc}} + \Delta E_{\text{atom}} + \cdots, \end{align*}

where various terms have the following interpretation.

Chemical energy, \(E_{\text{chem}} \text{,}\)
Nuclear energy, \(E_{\text{nuc}} \text{,}\)
Atomic random motion, \(E_{\text{atom}} \text{,}\)
Molecular rotational energy, \(E_{\text{mol.rot.}} \text{,}\) etc.

Subsection 24.1.6 Adiabatic Work and Internal Energy

Joule conducted experiments on the effect of stirring on the change in the state of water as determined from the change in the temperature of water. He found that, if the container is thermally insulated, the amount of work associated with the change of the state of water was independent of how the work was performed.

\begin{equation} W_{if} = U_f - U_i \ \ \ \text{(Adiabatic)}\tag{24.8} \end{equation}

This is what you expect from the first law of thermodynamics when \(Q = 0\text{.}\) The work here is also called adiabatic work. The adiabatic work can be used to find internal energy of a system with respect to a reference state, called the standard state.

If we set the internal energy of the standard state as \(U_0\text{,}\) then the internal energy of any arbitrary state A can be defined by appropriate adiabatic process.

\begin{equation} U_A = U_0 - W_{\text{standard-to-A}} \ \ \ \text{(in an adiabatic process)}\tag{24.9} \end{equation}

If no adaiabatic process can take you from the standard state to state A, you gan think of going from standard to some other state B and then from B to A, then we will get the internal energy at for state A by

\begin{equation} U_A = U_B - W_{\text{B-to-A}} = U_0 - W_{\text{standard-to-B}} - W_{\text{B-to-A}}.\tag{24.10} \end{equation}

This way, you can find the internal energy of all states of the system. We say that internal energy can be defined for every state and hence internal energy is said to be a state property.

Subsection 24.1.7 (Calculus) Infinitesimal First law of thermodynamics

The first law of thermodynamics can be applied to any system in the universe. Suppose a system A interacts with the another system B such that in an infinitesimal time \(dt\) an infinitesimal amount of heat \(\delta Q \) flows into A and an infinitesimal amount of work \(\delta W \) is done by A. Then, the first law of thermodynamics says that the internal energy of A will change by \(dU\text{,}\)

\begin{equation} dU = \delta Q - \delta W,\tag{24.11} \end{equation}

where I have used different symbols for infinitesimals for \(U \) and for \(Q\) and \(W\) to indicate that while A has definite values of \(U \) in each state of A since \(U \) is a state function, \(Q\) and \(W\) are not state variables and A does not have any definite values of \(Q\) and \(W\text{.}\)

This infinitesimal equation is applicable to all closed systems. In a hydrostatic system, such as gas in a tank, work is done as a result of change of volume. Therefore, in these systems we can write the energy involved in the work on the system in another form. This type of system is a very useful system for exploring quantitative implications of thermodynamic principles in significant detail. Many of the examples in this book will come from these systems.

To derive the form of the first law of thermodynamics in hydrostatic systems, consider a tank of gas in equilibrium with the environment. Let the tank have a freely movable piston and the conduct heat so that initially, say \(t=0\text{,}\) the pressure \(p_\text{in}\) inside the gas is equal to the pressure outside \(p_\text{out}\text{,}\) and temperature \(T_\text{in}\) inside the gas is equal to the temperature \(T_\text{out}\) outside.

We can denote the common pressure by \(p\) and the common temperature by \(T\text{.}\) Suppose we pull the piston outward very slowly so that the volume of the gas increases by amount \(dV\) but the pressure in the gas is maintained at \(p\) all the time.

The gas will do a work \(-pdV\) and an infinitesimal amount of heat \(dQ\) will enter the gas during this process. Therefore the change in internal energy of the gas for an infinitesimal process in this system will be given by the following relation.

\begin{equation} dU = dQ - pdV. \tag{24.12} \end{equation}

This is the infinitesimal form of the First Law of Thermoidynamics. For finite changes in state, this has to be integrated over the path of the process. Suppose, a process, changes the state of a gas from \((p_1, V_1)\) to \((p_2, V_2)\) along some curve in the \((p,V)\)-plane. Then an integration over the path of the process will give us the change in internal energy.

\begin{equation} \Delta U = \int_{\text{process}}\,dQ - \int_{\text{process}}\,p\,dV.\tag{24.13} \end{equation}

Prev Top Next