Simple Harmonic Oscillator

Section 13.2 Simple Harmonic Oscillator

Oscillatory motions are ubiquitous is nature, from the to and fro swaying of high-rise buildings to back and forth motion of pendulums, to vibrations of atoms in molecules, vibrations of guitar string, just to name a few.

A block attached to a spring provides an ideal model system to study harmonic oscillations. We often call this model system a simple harmonic oscillator (SHO). In real blocks attached to spring, friction and drag forces take away energy and damp the motion of the block, eventually stopping it. But, in this section, we will not worry about these effects. As a result, we will get a perpetual motion - the block attached to an ideal spring will oscillate for ever! In a later section we will address damping as well as how additional energy can be put into the block to keep it going.

Consider a block A of mass \(m\) attached to a spring of spring constant \(k\) placed on a horizontal frictionless surface. The other end of the spring is attached to an infinite-mass immovable support B.

The spring has a natural length, which we can call its equilibrium length. When spring is extended or shortened, the spring pulls in or pushes out at the two ends by a force, whose magnitude \(F_{s}\) is equal to the amount \(\Delta l\) by which the length is different from the equilibrium length.

\begin{equation} F = k\,\Delta l.\tag{13.2} \end{equation}

The direction of this force is from the current location of the end of the spring to the point at which the spring has the natural length. Another way to look at the spring force is that the force between objects at the two ends of the spring is attractive when the spring is stretched and repulsive when the spring is compressed.

Suppose the spring is oriented along \(x\)-axis and you pull the block of mass \(m\) by a distance \(x_0\) from its equilibrium and give it a push so that its starting speed is \(v_0\text{,}\) we will show below that the resulting motion is a sinusoidally oscillatory motion with \(x\) between \(x=-A\) and \(x=+A\) with

\begin{equation} A = \sqrt{ x_0^2 + \left( v_0/\omega \right)^2 },\tag{13.3} \end{equation}

with period

\begin{equation} T = 2\pi \sqrt{ \dfrac{m}{k} },\tag{13.4} \end{equation}

and frequency

\begin{equation} f = \frac{1}{T} = \frac{1}{2\pi} \sqrt{ \dfrac{k}{m} }.\tag{13.5} \end{equation}

Frequency tells us the number of repeat of the entire cycle of motion per unit of time. Often, we need to represent cycle of motion by a change of angle of a sine or cosine by \(2\pi\) radians. Then, we use what is called angular frequency, which is number of \(2\pi\) radians per unit time that such as funnction representing the motion undergoes. Angular frequency is usually denoted by \(\omega\text{.}\)

\begin{equation} \omega = 2\pi f = \sqrt{ \dfrac{k}{m} }.\tag{13.6} \end{equation}

Quantity \(A\) is called amplitude of the motion. Clearly, if you have a spring of known spring constant \(k\text{,}\) then you can find the mass of any object attached to it from measuring the period of the corresponding oscillations!

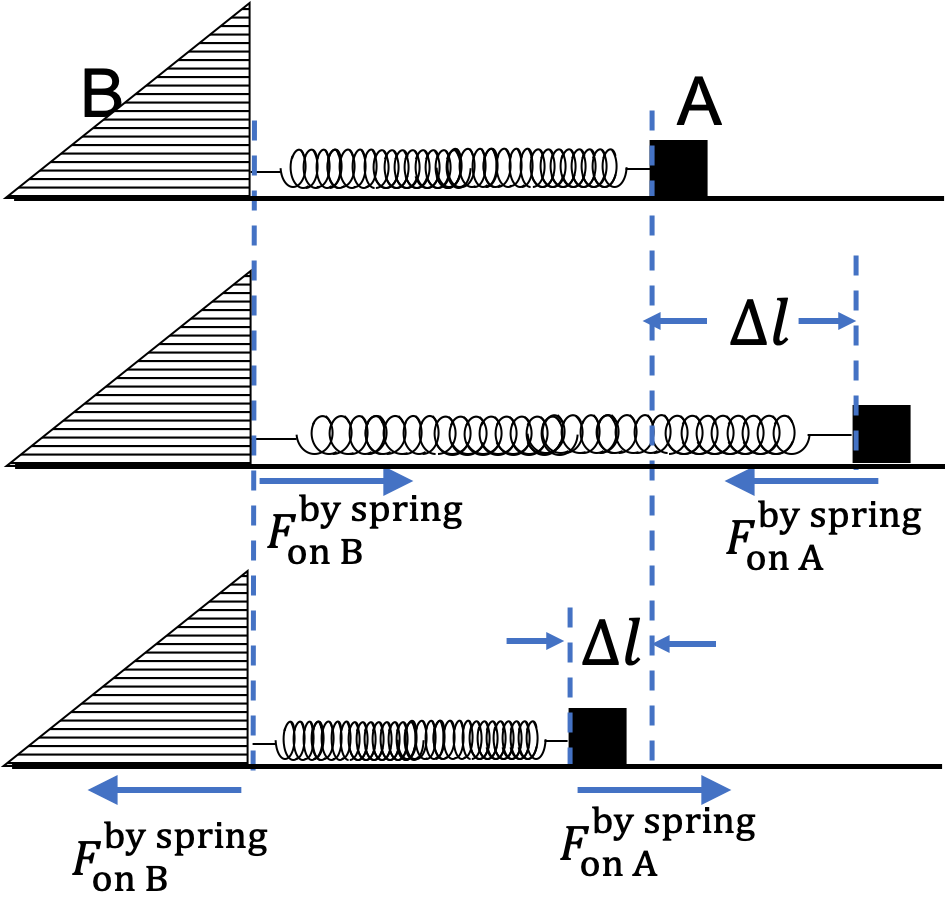
Example 13.5. Mass of an Astronaut from Harmonic Motion.

Astronauts must keep a good record of their masses. Th normal bathroom scales that use gravity to get mass would not work in space. Instead, mass can be obtained from \(T = 2\pi\sqrt{m/k}\) of a spring/mass oscillations. In this method, we find the mass of an astronaut by strapping the astronaut to a chair which is attached to a spring, and observing the motion.

The mass of the chair is \(200\text{ kg}\text{.}\) When astronaut is not in the chair, the period of oscillation is \(1.50\text{ sec}\text{.}\) The period changes to \(1.75\text{ sec}\text{.}\)

What is the mass of the astronaut?

Answer.

\(72.2\text{ kg}\text{.}\)

Solution.

Let \(M\) be the mass of the astronaut. Thinking of \(T = 2\pi\sqrt{m/k}\) as \(T\propto\sqrt{m}\text{,}\) gives us the following ratio

\begin{equation*} \dfrac{T_1}{T_2} = \sqrt{ \dfrac{M_1}{M_2} }\ \ \Longrightarrow\ \ M_2 = \left( \dfrac{T_2}{T_1} \right)^2\, M_1. \end{equation*}

Setting \(M_1 = 200\text{,}\) \(M_2 = M + 200\text{,}\) \(T_1=1.50\) and \(T_2=1.75\) we have

\begin{equation*} M = \left( \dfrac{1.75}{1.50} \right)^2 \times 200 - 200 = 72.2\text{ kg}. \end{equation*}

Subsection 13.2.1 Equation of Motion and Solution

To study the motion of the block analytically, we choose a coordinate system that has its positive \(x\)-axis pointed in the direction in which the spring stretches and we place the origin at the place where the block is located when spring is in its relaxed state.

Figure 13.6. Using coordinates to express the spring force analytically, \(F_x = - k x\text{.}\)

Let \(x \) denote the \(x \) coordinate of the block at instant \(t \text{.}\) With the arrangement in Figure 13.6, when the block’s position has \(x \gt 0 \text{,}\) the force on the block is pointed left, i.e., \(F_x \lt 0\text{,}\) and when the block’s position has \(x \lt 0\text{,}\) we have \(F_x \gt 0\text{,}\) where \(F_x\) is the \(x \) component of the force vector \(\vec F\) as usual. Therefore, force by spring has \(x\)-component given by

\begin{equation} F_x = -k\, x.\tag{13.7} \end{equation}

Therefore, \(x\)-equation of motion of the block is

\begin{equation} m a_x = - kx.\tag{13.8} \end{equation}

We would like to get a formula that tells us \(x(t) \) for given initial position and velocity, \(x_0\) and \(v_0\text{.}\) This is called solving the equation of motion. If you solve Eq. (13.8) for acceleration, they don’t take you anywhere, since \(a_x\) is actually second derivative of \(x\) with respect to time \(t\text{.}\)

\begin{equation*} x(t) = -\dfrac{m}{k}\, a_x = -\dfrac{m}{k}\, \frac{d^2x}{dt^2}. \end{equation*}

That is, you need to think of Eq. (13.8) as a differential equation and solve that differential equation. We will not do that here. We will just borrow the solution from the folks who have solved this equation.

The solution is more compactly written if we replace \(k/m\) by another symbol, actually, the square of a symbol \(\omega^2\text{,}\) since we want to make sure \(k/m\) is always positive regardless of the sign of \(\omega\text{.}\)

\begin{equation} \omega^2 = \sqrt{\dfrac{k}{m}}.\tag{13.9} \end{equation}

Then, position of the block that starts at \(x=x_0\) and \(x\)-component of the velocity \(v_x=v_0\) is completely determined by

\begin{equation} x(t) = x_0\, \cos(\omega t) + \dfrac{v_0}{\omega}\sin(\omega t).\tag{13.10} \end{equation}

The oscillator moves about the origin symmetrically. The largest \(x\) away from the equilibrium is called the amplitude, which is obtained by combining the coefficients of the cosine and sine terms as follows. The amplitude is usually denoted by \(A\text{.}\)

\begin{equation} A = \sqrt{ x_0^2 + \left( v_0/\omega \right)^2 }.\tag{13.11} \end{equation}

The velocity at intstant \(t \) is given by

\begin{equation} v_x(t) = v_0\, \cos(\omega t) - \omega\,x_0\, \sin(\omega t),\tag{13.12} \end{equation}

from which we get the largest speed in the motion to be

\begin{equation} \text{Largest speed } = \sqrt{v_0^2 + \left(\omega^2 x_0^2\right)^2 },\tag{13.13} \end{equation}

which occurs when the block passes through the equilibrum position, i.e., \(x=0\text{.}\)

Contrast these formulas for \(x\) and \(v\) to the constant acceleration motion for acceleration \(a_x \text{.}\)

\begin{align*} \text{Constant}\amp \text{ Acceleration Motion:}\\ \amp x(t) = x_0 + v_0\, t + \dfrac{1}{2}\, a_x\, t^2, \\ \amp v(t) = v_0 + a_x\, t. \end{align*}

We don’t have this situation here. The acceleration of a simple harmonic oscillator oscialltes in time and is definitely not constant.

Subsection 13.2.2 Multiple Ways of Writing the Solution

The solution in Eq. (13.10) is good for some purposes but not convenient for some other purposes. For instance, if we wanted to know the furthest from the equilibrium the block will go, its not \(x_0\text{,}\) and it is not clear right away how we would get the answer. There is another way to write a sum of cosine and sine of the same argument using the trig formulas for sum of angles.

For instance, we can write Eq. (13.10), which we now refer to as two-amplitudes form, also in the following form, which we will call amplitude-phase form.

\begin{equation} x(t) = A\,\cos(\omega t + \phi),\tag{13.14} \end{equation}

where \(A\) is the amplitude and \(\phi\) the phase constantphase. The argument of cosine itself is called the phase of the oscillator. Then, the velocity is

\begin{equation} v(t) = -\omega A\,\sin(\omega t + \phi),\tag{13.15} \end{equation}

Another way to write in amplitude-phase form is as a sine function.

\begin{equation} x(t) = B\,\sin(\omega t + \phi_s),\tag{13.16} \end{equation}

Our convention is to write as positive amplitude times a cosine and use the following to convert anything written in sine to cosine, which makes writing in sine superflous.

\begin{equation} \sin(\theta) = \cos(\theta - \pi/2).\tag{13.17} \end{equation}

If we find an expression with negative amplitude times a cosine, we can convert that to positive amplitude times cosine by

\begin{equation} -\cos(\theta) = \cos(\theta - \pi).\tag{13.18} \end{equation}

The new constants \(A\) and \(\phi\) are related to initial position \(x_0\) and velocity \(v_0\) as in Eq. (13.10). To find the relation, we expand the right side in this equation,

\begin{equation*} A\,\cos(\omega t + \phi) = A\, \cos\omega t\,\cos\phi - A\, \sin\omega t\,\sin\phi, \end{equation*}

and compare the result to Eq. (13.10). This gives the following two equations.

\begin{align*} \amp A\,\cos\phi = x_0,\\ \amp A\,\sin\phi = -\dfrac{v_0}{\omega}. \end{align*}

Squarring and adding these will give us \(A^2\) and dividing will give us \(\tan\phi\text{.}\) We take the notation that \(A\) be positive.

\begin{align*} \amp A = \sqrt{ x_0^2 + \dfrac{v_0^2}{\omega^2} },\\ \amp \tan\phi = -\dfrac{v_0}{\omega x_0}. \end{align*}

The velocity corresponding to the form (13.14) is

\begin{equation} v_x(t) = -\omega\, A\,\sin(\omega t + \phi).\tag{13.19} \end{equation}

This says that the velocity oscillates between \(-\omega A\) and \(\omega A\text{.}\) Clearly, oscillator has turns in its motion, where velocity must be zero. Turning point at \(x=+A\) and \(x=-A\) correspond to \(v=0\text{.}\)

Subsection 13.2.3 Meaning of \(\omega \)

The meaning of \(\omega\) can be gleaned from the periodic behavior of the solution given in Eq. (13.10). We observe that

\begin{align*} x\left(t + \dfrac{2\pi}{\omega}\right) \amp = x_0\, \cos\left[\omega\,\left(t + \dfrac{2\pi}{\omega}\right) \right] + \dfrac{v_0}{\omega}\sin\left[\omega\,\left(t + \dfrac{2\pi}{\omega}\right) \right],\\ \amp = x_0\, \cos \left( \omega t + 2\pi \right) + \dfrac{v_0}{\omega} \sin\left( \omega t + 2\pi \right), \\ \amp = x_0\, \cos(\omega t) + \dfrac{v_0}{\omega}\sin(\omega t) = x(t) \end{align*}

That is, the position is periodic in time with a period \(T = \dfrac{2\pi}{\omega}\text{.}\) Furthermore, velocity in Eq. (13.12) is also periodic with the same period. That is, the motion at \(t + \dfrac{2\pi}{\omega}\) is identical to the motion at \(t\text{.}\)

\begin{equation} T = \dfrac{2\pi}{\omega}.\tag{13.20} \end{equation}

Therefore, we can state \(\omega \) in terms of the period of the oscillator.

\begin{equation} \omega = 2\pi\,\dfrac{1}{T}.\tag{13.21} \end{equation}

Now, in one period \(T\text{,}\) an oscillator will complete one cycle. Therefore, \(1/T\) would be the number of cylces in unit time. This is called frequency of the oscillator and denoted by \(f\text{,}\) and sometimes by the Greek letter “nu”, \(\nu \text{.}\)

\begin{equation} f = \dfrac{1}{T}.\tag{13.22} \end{equation}

Now, writing \(\omega\) in terms of the frequency \(f\text{,}\) we have

\begin{equation} \omega = 2\pi f,\tag{13.23} \end{equation}

where \(2\pi \) is an angle in radian. Therefore, \(\omega \) is frequency such that for each cycle we count \(2\pi\) radian instead of one. This is what you would expect of angle variable for something moving in a circle. That is why we call \(\omega\) the angular frequency. Note that the block attached to a spring is not moving in circle - its just an interpretation of \(\omega\) as it relates to the regular frequency, which is the number of cycles of oscillations per unit time.

The unit of period \(T \) is seconds. Therefore, the unit of regular frequency, \(f \) is per second or cycles per second, which is given its own name, Hertz (Hz). The unit for \(\omega\) is radians per second.

Subsection 13.2.4 Amplitude and Phase

The solution in the form (13.14) tells us that \(x \) will oscillate between \(+ A \) and \(-A \) since cosine will oscillate between \(+1 \) and \(-1\) as illustrated in Figure 13.7. That is, \(A \) is the amplitude of the oscillation.

Figure 13.7. The plot of the position of an oscillator versus time showing the amplitude. The plot of \(x \) versus \(t \) was made with \(\phi = 0\) and \(\omega = 1 \text{.}\)

In the solution in the form Eq. (13.14), the argument of the cosine, viz., \((\omega t + \phi) \) is called phase of the oscillator, and \(\phi \) is called the phase constant. We usually think of phase as an angle in a circle as illustrated in Figure 13.8.

Figure 13.8. The left side of the figure shows a block attached to a spring and labels the block at various points in its periodic motion. One cycle of motion here could be thought in the order, A-B-C-D-E-F. Note that although C and E are same point in space, the block is moving to the left when at C, snd moving to the right when at E - that is, the state of motion of the block is different at the the two instants. The cylce can also be represented by showing the phase as angle \(\theta = (\omega t + \phi) \) of a *fictitious vector* rotating in a circle at rate \(\omega\text{.}\)

But what about \(\phi\text{?}\) How to think about it? It has the information about where in the cycle, the oscillator is. Actually, \(\phi\) is best understood by comparing two identical oscillators, oscillator 1 with \(\phi = 0\) and oscillator 2 with \(\phi = -\pi/2\text{,}\) as presented in Figure 13.9.

\begin{align*} \amp x_1 (t) = A\,\cos(\omega t ), \\ \amp x_1 (t) = A\,\cos(\omega t -\pi/2) = A\,\sin(\omega t), \end{align*}

From the pictures of sine and cosine, you can see that cosine at \(\theta=0\) is at the same place in cycle as sine would be at \(\theta=\pi/2\text{.}\) You might say sine is behind by \(\pi/2\) radian. that is oscillator 2 with \(\phi=-\pi/2\) is \(\pi/2\) radian behind oscillator 1.

Figure 13.9. Comparing the motions of two oscillators with different phase constants. In each case, the arrow from the center to the arc of the circle rotates with angle with respect to the positive \(x \) axis as \(\theta(t) = \omega t + \phi\text{.}\) This arrow is called a phasor and the angle of the phasor is called the phase of the oscillator. Since the two oscillators have the same frequency \(\omega \text{,}\) the two phasors rotate at the same rate, but since block 2 is behind block 1 by a phase constant of \(\pi/2\) radians, the motion of block 2 is quarter cycle behind in its motion relative to block 1.

Example 13.10. Reading Harmonic Oscillator Solutions in Two-Amplitudes Form.

A harmonic oscillator oscillates on \(x\) axis about the origin with its \(x\) coordinate given by

\begin{equation*} x = 3\, \cos\,\left( 15\, t \right) + 4\, \sin\,\left( 15\, t \right) \end{equation*}

where \(t\) is in seconds and \(x\) in \(\text{cm}\text{.}\)

(a) What is the amplitude of the oscillations?

(b) What is the angular frequency of the oscillator?

(d) What is the period of the oscillator?

(e) Where is the oscillator at \(t = 0\text{?}\)

(f) How fast is the oscillator moving at \(t = 0\) and which way? Note: from the formula of \(x\text{,}\) the \(x\) component of velocity is

\begin{equation*} v = -45\, \sin\,\left( 15\, t\right) + 60\, \cos\,\left( 15\, t \right). \end{equation*}

If you have Calculus background, try deriving this yourself.

Answer.

(a) \(5\text{ cm}\text{,}\) (b) \(15\text{ sec}^{-1}\text{,}\) (c) \(11.94\text{ cycles}\text{,}\) (d) \(0.42\text{ sec} \text{,}\) (e) \(3\text{ cm}\text{,}\) (f) \(60\text{ cm/sec}\) in the direction of positive \(x\) axis.

Solution.

(a) From the two-amplitudes form of the solution, we get the amplitude immediately.

\begin{equation*} \text{Amplitude } = \sqrt{ (3\text{ cm})^2 + (4\text{ cm})^2 } = 5\text{ cm}. \end{equation*}

(b) From the argument of cosine or sine, here, we see how the periodic motion varies in time. Equating the time part to \(\omega t\) we immediately get \(\omega\text{.}\)

\begin{equation*} \omega = 15\text{ sec}^{-1}. \end{equation*}

\begin{equation*} f = \dfrac{\omega}{2\pi} = \dfrac{15}{2\pi} = 2.387\text{ Hz}. \end{equation*}

That is, 2.387 cycles each second. Therefore, we will have

\begin{equation*} N = 2.387\text{ Hz} \times 5\text{ sec} = 11.94\text{ cycles}. \end{equation*}

(d) Inverting the frequency gives the period.

\begin{equation*} T = \dfrac{1}{f} = \dfrac{1}{2.387\text{ Hz}} = 0.42\text{ sec}. \end{equation*}

(e) Set \(t=0\) in the given \(x\) to get

\begin{equation*} x_0 = 3\text{ cm}. \end{equation*}

(f) Set \(t=0\) in the given \(v\) to get

\begin{equation*} v_0 = 60\text{ cm/sec}. \end{equation*}

Since \(v_0\) is positive, the block is moving in the direction of positive \(x\) axis.

Example 13.11. Reading Harmonic Oscillator Solutions in Amplitude-Phase Form.

A harmonic oscillator oscillates on \(x\) axis about the origin with its \(x\) coordinate given by

\begin{equation*} x = 10\, \cos\,\left( 15\, t + \dfrac{\pi}{4}\right), \end{equation*}

where \(t\) is in seconds and \(x\) in \(\text{cm}\text{.}\)

(a) What is the amplitude of the oscillations?

(b) What is the angular frequency of the oscillator?

(d) What is the period of the oscillator?

(e) Where is the oscillator at \(t = 0\text{?}\)

(f) How fast is the oscillator moving at \(t = 0\) and which way? Note: from the formula of \(x\text{,}\) the \(x\) component of velocity in \(\text{cm/s}\) is

\begin{equation*} v = -150\, \sin\,\left( 15\, t + \dfrac{\pi}{4}\right). \end{equation*}

If you have Calculus background, try deriving this yourself.

Answer.

(a)\(10\text{ cm}\text{,}\) (b)\(15\text{ sec}^{-1}\text{,}\) (c)\(11.94\text{ cycles}\text{,}\) (d)\(0.42\text{ sec} \text{,}\) (e)\(7.07\text{ cm}\text{,}\) (f)\(106\text{ cm/sec}\) towards the origin.

Solution.

(a) From the amplitude/phase form of the solution, we get the amplitude immediately.

\begin{equation*} \text{Amplitude } = 10\text{ cm}. \end{equation*}

(b) From the argument of cosine, here, we see how the periodic motion varies in time. Equating the time part to \(\omega t\) we immediately get \(\omega\text{.}\)

\begin{equation*} \omega = 15\text{ sec}^{-1}. \end{equation*}

\begin{equation*} f = \dfrac{\omega}{2\pi} = \dfrac{15}{2\pi} = 2.387\text{ Hz}. \end{equation*}

That is, 2.387 cycles each second. Therefore, we will have

\begin{equation*} N = 2.387\text{ Hz} \times 5\text{ sec} = 11.94\text{ cycles}. \end{equation*}

(d) Inverting the frequency gives the period.

\begin{equation*} T = \dfrac{1}{f} = \dfrac{1}{2.387\text{ Hz}} = 0.42\text{ sec}. \end{equation*}

(e) Set \(t=0\) in the given \(x\) to get

\begin{equation*} x_0 = 10\, \cos\,\left( \dfrac{\pi}{4}\right) = 7.07\text{ cm}. \end{equation*}

(f) Set \(t=0\) in the given \(v\) to get

\begin{equation*} v_0 = -150\, \sin\,\left( \dfrac{\pi}{4}\right) = -106\text{ cm/sec}. \end{equation*}

That is, it has speed \(106\text{ cm/sec}\) and moving to the left.

Example 13.12. Writing Harmonic Oscillator Solutions in Alternate Forms.

The solution of a Simple Harmonic Motion can be written in three ways:

\begin{align*} x(t) \amp = C_1\ \cos(\omega t) + C_2\ \sin(\omega t)\\ \amp = A \cos(\omega t + \phi_c)\\ \amp = B \sin(\omega t + \phi_s) \end{align*}

Find the relations among (a) \(C_1\text{,}\) \(C_2\text{,}\) \(A\text{,}\) \(\phi_c\text{,}\) (b) \(C_1\text{,}\) \(C_2\text{,}\) \(B\text{,}\) \(\phi_s\text{,}\) and (c) \(A\text{,}\) \(\phi_c\text{,}\) \(B\text{,}\) \(\phi_s\text{.}\) Trig formulas \(\cos(A+B) = \cos\,A\cos\,B-\sin\,A\sin\,B \text{,}\) \(\sin(A+B)=\sin\,A\cos\,B+\sin\,B\cos\,A\text{,}\) and \(\sin(\theta + \pi/2) = \cos\,\theta \) will be helpful.

Answer 1. (a)

(a) \(A\cos\,\phi_c = C_1\text{,}\) \(A\sin\,\phi_c = C_2\text{,}\) \(A = \sqrt{ C_1^2 + C_2^2 }\text{,}\) \(\tan\,\phi_c = -\dfrac{C_2}{C_1}\text{.}\)

Answer 2. (b)

(b) \(B \sin\,\phi_s = C_1\text{,}\) \(B \cos\,\phi_s = C_2\text{,}\) \(B = \sqrt{ C_1^2 + C_2^2 }\text{,}\) \(\tan\,\phi_s = \dfrac{C_1}{C_2}\text{.}\)

Answer 3. (c)

Solution 1. (a)

(a) Let us expand \(A \cos(\omega t + \phi_c)\text{.}\)

\begin{equation*} A \cos(\omega t + \phi_c) = (A\cos\,\phi_c)\, \cos (\omega t) - (A\sin\,\phi_c)\, \sin (\omega t). \end{equation*}

Equate the coefficients of \(\cos(\omega t)\) and similarly for \(\sin(\omega t)\) in this expression to that in \(C_1\ \cos(\omega t) + C_2\ \sin(\omega t)\) we get

\begin{align*} A\cos\,\phi_c \amp = C_1, \\ -A\sin\,\phi_c \amp = C_2. \end{align*}

From this we can get

\begin{align*} \amp A = \sqrt{ C_1^2 + C_2^2 }, \\ \amp \tan\,\phi_c = -\dfrac{C_2}{C_1}. \end{align*}

Solution 2. (b)

(a) Let us expand \(B \sin(\omega t + \phi_s)\text{.}\)

\begin{equation*} B \sin(\omega t + \phi_s) = (B \cos\,\phi_s)\, \sin (\omega t) + (B\sin\,\phi_s)\, \cos (\omega t). \end{equation*}

Equate the coefficients of \(\cos(\omega t)\) and similarly for \(\sin(\omega t)\) in this expression to that in \(C_1\ \cos(\omega t) + C_2\ \sin(\omega t)\) we get

\begin{align*} B \sin\,\phi_s \amp = C_1, \\ B \cos\,\phi_s \amp = C_2. \end{align*}

From this we can get

\begin{align*} \amp B = \sqrt{ C_1^2 + C_2^2 }, \\ \amp \tan\,\phi_s = \dfrac{C_1}{C_2}. \end{align*}

Solution 3. (c)

(c) Since \(\sin(\theta + \pi/2) = \cos\,\theta\text{,}\) we can write both of then in either cosines or sines forms. Let us write the cosine into sine to get

\begin{equation*} A\cos(\omega t + \phi_c) = A\sin(\omega t + \phi_c +\pi/2). \end{equation*}

Equating this to the sine-form given, we immediately get

\begin{equation*} B = A,\ \ \phi_s = \phi_c +\pi/2. \end{equation*}

Example 13.13. Harmonic Oscillator Solution for Given Initial Position and Velocity.

A block of mass \(2\text{ kg}\) is attached to a spring of spring constant \(32\text{ N/m} \) and placed on a frictionless surface. The other end of the spring is attached to a fixed support. At \(t=0\text{,}\) the block is hit with a hammer such that it instantaneously gains speed of \(0.8\text{ m/s}\) and starts to compress the spring. You can assume that at \(t=0\) the block is at the equilibrium position.

(a) With \(x\) axis along the spring and positive \(x\) axis in the direction in which the spring stretches, find the position and velocity of the block at an arbitrary instant \(t\text{.}\)

(b) What is the amplitude of the oscillations?

Answer.

(a) \(x(t) = - 0.2\text{ m }\,\sin(4\,t )\text{,}\) \(v(t) = - 0.8 \text{ m/s } \,\cos(4\,t )\text{,}\) (b) \(0.2\text{ m } \text{.}\)

Solution 1. (a)

Since the block at \(t=0\) is moving in the opposite direction to the positive \(x\) axis, we have the following initial condition on the \(x\) component of the velocity

\begin{equation*} v_0 = - 0.8\text{ m/s}. \end{equation*}

The initial position is \(x_0 = 0\) since it is at the equilibrium position. From the given mass and spring constant, we get the angular frequency to be

\begin{equation*} \omega = \sqrt{ \dfrac{k}{m} } = 4\text{ sec}^{-1}. \end{equation*}

Using these in the two-amplitudes-form of the solution we get

\begin{align*} \amp x(t) = - 0.2 \,\sin(4\,t ), \\ \amp v(t) = - 0.8 \,\cos(4\,t ), \end{align*}

where \(t\) is in \(\text{sec}\text{,}\) \(x\) in \(\text{m}\text{,}\) and \(v\) in \(\text{m/s}\text{.}\)

Solution 2. (b)

From \(x(t) = - 0.2\,\sin(4\,t ) \text{,}\) we see that \(x\) goes between \(- 0.2\text{ m } \) and \(+ 0.2\text{ m } \text{.}\) That is, the amplitude is \(0.2\text{ m } \text{.}\)

Example 13.14. Understanding Positions of Two Oscillators and Their Phasors.

Two oscillators of masses \(200\text{ g}\) and \(400\text{ g}\) oscillate with the same frequency. They move such that their positions from their corresponding equilibrium points are given by the following two functions (\(t\) in seconds, \(x\) in cm) \(x_1\) and \(x_2\) respectively.

\begin{align*} \amp x_1 = 2 \cos(t)\\ \amp x_2 = 2 \sin(t) \end{align*}

(a) What are the angular frequencies, amplitudes and phase constants of the two oscillators?

(b) What were their positions and velocities at the initial time \(t=0\text{?}\)

Answer.

(a) \(\omega_1 = 1\text{ rad/s}\text{,}\) \(A_1 = 2\text{ cm}\text{,}\) \(\phi_1 = 0\text{,}\) \(\omega_2 = 1\text{ rad/s}\text{,}\) \(A_2 = 2\text{ cm}\text{,}\) \(\phi_1 = -\dfrac{\pi}{2}\text{;}\) (b) \(x_1(0) = 2\text{ cm}\text{,}\) \(x_2(0) = 0\) , \(v_{1}(0) = 0 \text{,}\) \(v_{2}(0) = 2\text{ cm/s}\text{,}\) (c) Two arrows, one at one radian counterclockwise from positive \(x \) axis, and the other \(\pi/2\) radian behind in the cycle.

Solution 1. (a)

Comparing with the solution \(x = A \cos(\omega t + \phi)\text{,}\) we read off the values for the first oscillator.

\begin{equation*} \omega_1 = 1\text{ rad/s},\ \ A_1 = 2\text{ cm},\ \ \phi_1 = 0. \end{equation*}

The second oscillator is given in sine. So, we first write it as a cosine with positive multiplying factor, and then read off the values.

\begin{equation*} x_2 = 2\,\sin(t) = 2\,\cos(t-\pi/2). \end{equation*}

Therefore,

\begin{equation*} \omega_2 = 1\text{ rad/s},\ \ A_2 = 2\text{ cm},\ \ \phi_2 = -\dfrac{\pi}{2}. \end{equation*}

Solution 2. (b)

(b) The initial positions are just the values of \(x \) at \(t = 0\text{.}\) The velocities are

\begin{align*} \amp v_1 = -2\,\sin(t) \longrightarrow v_1(0) = 0. \\ \amp v_2 = 2\,\cos(t) \longrightarrow v_2(0) = 2\text{ cm/s}. \end{align*}

Solution 3. (c)

Figure 13.15. Figure for Example 13.14(c).

Exercises 13.2.5 Exercises

1. Angular Frquesncy, Frequency, and Period of a GHarmonic OScillator.

A harmonic oscillator of mass \(200\,\text{grams}\) is attached to a spring of spring constant \(100\, \text{N/m}\text{.}\) Find (a) angular frequency, (b) frequency and (c) time period.

Answer.

(a) \(22.4\, \text{rad/sec}\text{,}\) (b) \(3.56\, \text{Hz}\text{,}\) (c) \(0.28\,\text{sec}\text{.}\)

Solution.

\begin{align*} \amp \textrm{(a) Angular frequency:}\ \ \omega = \sqrt{\frac{k}{m}} = \sqrt{\frac{100\ \textrm{N/m}}{0.200\ \textrm{kg}}} = 22.4\ \textrm{rad/sec}.\\ \amp \textrm{(b) Frequency:}\ \ f = \frac{\omega}{2\pi} =\frac{22.4\ \textrm{rad/s}}{2\pi} = 3.56\ \textrm{Hz}.\\ \amp \textrm{(c) Time Periond:}\ \ T = \frac{1}{f} = \frac{1}{3.56\ \textrm{Hz}} = 0.28\ \textrm{s}.\\ \end{align*}

2. Comparing Position and Velocity of Two Oscillators with Different Phases.

Two oscillators of masses 200 g and 400 g oscillate with the same frequency. They move such that their positions from their corresponding equilibrium points are given by the following two functions (\(t\) in seconds, \(x\) in cm) \(x_1\) and \(x_2\) respectively.

\begin{align*} \amp x_ 1 = 2 \cos(t)\\ \amp x_ 2 = 2 \sin(t) \end{align*}

(a) What are the angular frequencies, amplitudes and phase constants of the two oscillators?

(b) What were their positions and velocities at the initial time \(t=0\text{?}\)

(c) Plot the positions of the two oscillators versus time on the same graph, and interpret which oscillator is ahead, and by how much.

Answer.

(a) ang.freq. = 1 rad/s, ampl. = 2 cm, phase const. = 0 and \(\pi\) radians; (b) \(x_1(0)\) = 2 cm; \(x_2(0)\) = -2 cm; \(v_{1x}(0) = 0 = v_{2x}(0)\text{;}\)

Solution 1. a

Both oscillators have the angular frequency of 1 rad/sec. The frequencies are also same, given by \(1/2\pi = 0.159\) Hz.

For the phase constant, we take one of the oscillators are the reference. Let the phase constant of \(x_1\) be 0. Then, we expressing \(x_2)\) also as cosine will help us compare the two phases.

\begin{equation*} x_2 = \sin(t) = \cos\left( t - \frac{\pi}{2}\right). \end{equation*}

This shows that the phase constant of \(x_2\) is \(-\pi/2\) rad.

Solution 2. b

The positions can be found by just putting in \(t=0\) in the given expressions. To find the velocity, which is the \(x\)-component of the velocity here, we will need to take a derivative before setting the value of \(t\) to zero.

\begin{align*} \amp x_1(0) = 1\\ \amp x_2(0) = 0 \\ \amp v_{1x}(0) = \left.\frac{dx_1}{dt}\right|_{t=0} = -\sin(0) = 0.\\ \amp v_{2x}(0) = \left.\frac{dx_2}{dt}\right|_{t=0} = \cos(0) = 1. \end{align*}

Solution 3. c

The plots in Figure 13.16 show that the peaks of \(x_1 = \cos(t)\) occur before the peaks of \(x_2 = \sin(t)\) by quarter of a cycle, which corresponds to and angle of \(\pi/2\) rad inside the argument for the cosine or sine.

3. Position Function of an Oscillator from Given Initial Conditions.

An oscillator of frequency \(20\) cycles per second starts \(3\) cm from the equilibrium so that spring is in stretched state and oscillator has initial velocity of \(40\,\pi\) cm/s pointed towards the equilibrium point. (a) Find \(x(t)\) for the oscillator. (b) What is the amplitude of the motion of the oscillator?

Answer.

(a) \(3\, \text{cm}\,\cos( 40\pi t) + (-1)\,\text{cm}\,\sin(40\pi t)\text{,}\) (b) \(\sqrt{10}\,\text{cm}\text{.}\)

Solution 1. a

We will use a combination of sine and cosine to work with.

\begin{equation} x(t) = A \cos(2\pi f t) + B \sin(2\pi f t),\tag{13.24} \end{equation}

where \(f = 20\) Hz, and we need to find \(A\) and \(B\) from the intial conditions on position and velocity. They are given as

\begin{equation*} x(0) = 3\ \textrm{cm};\ \ v_x(0) = -40\pi\, \textrm{cm/s}. \end{equation*}

Note the minus sign in \(v_x(0)\) to reflect the fact that the block is moving towards the negative \(x\)-axis at this instant. To find \(v_x(t)\) we take the time derivative of \(x(t)\) in Eq. (13.24). The initial conditions give the following conditions on \(A\) and \(B\text{.}\)

\begin{align*} \amp A = 3\ \textrm{cm} \\ \amp2\pi f B = -40\pi\, \textrm{cm/s}. \end{align*}

Therefore, we have the following for \(x(t)\text{.}\)

\begin{equation*} x(t) = (3\ \textrm{cm})\ \cos(40\pi t) - 1\,\text{cm}\, \sin(40\pi t). \end{equation*}

Solution 2. b

To find the amplitude of motion, we combine the amplitudes of cosine and sine terms in the solution as follows.

\begin{equation*} \text{Amplitude } = \sqrt{A_c^2 + A_s^2} = \sqrt{3^2 + 1^2} = \sqrt{10}\,\text{cm}. \end{equation*}

4. Motion of Oscillator from initial Displacement and Velocity in Same Directions.

An oscillator of frequency \(20\) cycles per second starts \(3\) cm from the equilibrium so that spring is in stretched state and oscillator has initial velocity of \(40\,\pi\) cm/s pointed away from the equilibrium point. (a) Find \(x(t)\) for the oscillator. (b) What is the amplitude of the motion of the oscillator?

Answer.

(a) \(3\, \text{cm}\,\cos( 40\pi t) + 1\,\text{cm}\,\sin(40\pi t)\text{,}\) (b) \(\sqrt{10}\,\text{cm}\text{.}\)

Solution 1. a

We will use a combination of sine and cosine to work with.

\begin{equation} x(t) = A \cos(2\pi f t) + B \sin(2\pi f t),\tag{13.25} \end{equation}

where \(f = 20\) Hz, and we need to find \(A\) and \(B\) from the intial conditions on position and velocity. They are given as

\begin{equation*} x(0) = 3\ \textrm{cm};\ \ v_x(0) = +40\pi\, \textrm{cm/s}. \end{equation*}

Note the plus sign in \(v_x(0)\) to reflect the fact that the block is moving towards the positive \(x\)-axis at this instant. To find \(v_x(t)\) we take the time derivative of \(x(t)\) in Eq. (13.25). The initial conditions give the following conditions on \(A\) and \(B\text{.}\)

\begin{align*} \amp A = 3\ \textrm{cm} \\ \amp2\pi f B = +40\pi\, \textrm{cm/s}. \end{align*}

Therefore, we have the following for \(x(t)\text{.}\)

\begin{equation*} x(t) = (3\ \textrm{cm})\ \cos(40\pi t) + 1\,\text{cm}\, \sin(40\pi t). \end{equation*}

Solution 2. b

To find the amplitude of motion, we combine the amplitudes of cosine and sine terms in the solution as follows.

\begin{equation*} \text{Amplitude } = \sqrt{A_c^2 + A_s^2} = \sqrt{3^2 + 1^2} = \sqrt{10}\,\text{cm}. \end{equation*}

5. Various Forms of the Simple Harmonic Oscillator Solution.

The solution of a Simple Harmonic Motion can be written in three ways:

\begin{align*} x(t) \amp = C_1\ \cos(\omega t) + C_2\ \sin(\omega t) \\ \amp = A \cos(\omega t + \phi_c)\\ \amp = B \sin(\omega t + \phi_s) \end{align*}

Find the relations among \(C_1\text{,}\) \(C_2\text{,}\) \(A\text{,}\) \(B\text{,}\) \(\phi_c\text{,}\) and \(\phi_s\text{.}\)

(Actually, there is also a complex representation that is very useful: \(C\,e^{i\,\omega\,t}\text{,}\) where \(C\) is a complex amplitude. )

Solution.

Let us first work out the relations between \(C_1\text{,}\) \(C_2\text{,}\) \(A\text{,}\) and \(\phi_c\text{.}\) We can start by expanding the \(\cos(\omega t + \phi_c)\) and compare with the expanded expression.

\begin{align*} \amp A \cos(\omega t + \phi_c) = A \cos(\phi_c) \cos(\omega t) - A \sin(\phi_c) \sin(\omega t). \end{align*}

Since only the time \(t\) is a variable, and \(\cos\omega t\) is independent of \(\sin\omega t\text{,}\) we equate the coefficients of these functions in the two representations to obtain

\begin{align*} \amp C_1 = A \cos(\phi_c).\\ \amp C_2 = - A \sin(\phi_c). \end{align*}

These relations give

\begin{align*} \amp A^2 = C_1^2 + C_2^2.\\ \amp \tan(\phi_c) =- \frac{C_2}{C_1}. \end{align*}

Since \(A\) is the amplitude of the oscillation, \(A\) is positive.

\begin{equation*} A = \sqrt{C_1^2 + C_2^2}. \end{equation*}

Similarly, we find

\begin{align*} \amp B = \sqrt{C_1^2 + C_2^2}.\\ \amp \cot(\phi_s) = \frac{C_2}{C_1}. \end{align*}

Therefore,

\begin{align*} \amp B = A = \sqrt{C_1^2 + C_2^2}.\\ \amp \cot(\phi_s) = \frac{C_2}{C_1} = -\tan(\phi_c). \end{align*}

While inverting the tangent we need to be vigilant about the quadrant in which the pair \((C_1, C_2)\) falls when \(C_1\) is along the \(x\)-axis and \(C_2\) along the \(y\)-axis of an abstract \(xy\)-plane.

Prev Top Next