Damped Harmonic Oscillator

Section 13.8 Damped Harmonic Oscillator

Any frictional force will damp the motion, but viscous drag is a particularly easier damping force to work with analytically.

\begin{equation} \vec F_{visc} = -b\ \vec v\ \ \ (b \ge 0), \tag{13.44} \end{equation}

where \(b\) is the proportionality constant that depends on the viscosity of the medium and the geometry of the moving object. We have a minus sign in Eq. (13.44) since drag opposes velocity.

Viscous forces of this type act on objects moving in a fluid, such as air, water, oil, etc., if their speeds are not too great. A viscous damping can also be implemented by pushing and pulling a plunger into a gas cylinder as shown in Figure 13.28(b). an arrangement called a dashpot.

Figure 13.28. Two mechanisms by which we can introduce linear damping force in Eq. (13.44). (a) Damping by drag from fluid, such as a liquid or gas, (b) Damping from a dashpot attached to the moving body, where the plunger pushes and pulls on a gas in the cylinder.

Subsection 13.8.1 Equation of Motion

We place \(x \) along the spring with positive \(x \) axis in the direction in which spring stretches and origin at the position of the block when in equilibrium. With these choices, the \(x\) component of the net force from the two forces on the damped block will be

\begin{equation} F_x = - k x - b v_x.\tag{13.45} \end{equation}

Therefore, equation of motion of a damped block is

\begin{equation} m a_x = - k x - b v_x.\tag{13.46} \end{equation}

Solving this as a differential equation gives us all possible motions of a damped harmonic oscillator.

Subsection 13.8.2 Three Types of Damped Oscillators

Solutions of Eq. (13.46) tell us about \(x \) at an arbitrary instant \(t\text{,}\) possibly in terms of given \(x_0\) and \(v_0 \text{,}\) the position and velocity at initial instant \(t=0\text{.}\) Once again, this can be done by treating Eq. (13.46) as differential equation. We will just borrow the solution found by advanced mathematics.

There are three types of solutions, depending upon the values of the parameters \(m\text{,}\) \(k\text{,}\) and \(b\text{.}\) Actually, only two effective parameters are needed. These are

\begin{align} \amp \text{Free angular frequency, } \omega = \sqrt{\dfrac{k}{m}},\tag{13.47}\\ \amp \text{Damping constant, } \gamma = \dfrac{b}{m}.\tag{13.48} \end{align}

Sometimes, formulas are written using another damping constant, \(\beta \text{,}\) instead of \(\gamma\text{.}\) For consistency of our treatment here, we will use \(\gamma\) in our formulas.

\begin{equation} \beta = \dfrac{\gamma}{2} \equiv \dfrac{b}{2m}.\tag{13.49} \end{equation}

Depending on the relative values of \(\omega \) and \(\gamma\text{,}\) we get either an oscillating behavior or some other motion. The solutions tell us that there are three types of motion possible.

\begin{align} \amp \text{Underdamped Oscillations: }\ \ \ \omega \gt \frac{\gamma}{2},\tag{13.50}\\ \amp \text{Overdamped Motion: }\ \ \ \omega \lt \frac{\gamma}{2},\tag{13.51}\\ \amp \text{Critically Damped Motion: }\ \ \ \omega = \frac{\gamma}{2}.\tag{13.52} \end{align}

Subsection 13.8.3 Underdamped Oscillator Solution

The underdamped solution can be written in many forms, but the following form is very useful in further understanding of what happens to the block as time passes.

\begin{equation} x(t) = A\,e^{-\gamma t/2}\, \cos( \omega^{\prime} t + \phi ),\tag{13.53} \end{equation}

where \(\omega^{\prime} \) is the oscilaltion angular frequency of the underdamped oscillator, given by

\begin{equation} \omega^{\prime} = \sqrt{ \omega^2 - \gamma^2/4 },\tag{13.54} \end{equation}

which shows that the underdamped oscillator oscillates at another frequency than the natural frequency, \(\omega\text{,}\) which was the frequency at which the non-damped oscillator oscillated. The constants \(A \) and \(\phi \) are related to the initial \(x_0\) and \(v_0 \text{.}\) They are very complicated and not very illuminating. Here, I will just list the equations from which you can deduce \(A \) and \(\phi\text{.}\)

\begin{align} \amp A\cos\,\phi = x_0,\tag{13.55}\\ \amp A\sin\,\phi = -\dfrac{v_0}{\omega^{\prime}} - \dfrac{\gamma}{2\omega^{\prime}}\,x_0. \tag{13.56} \end{align}

Figure 13.29 shows a plot of \(x \) versus \(t\) for an underdamped oscillator. Clearly, an underdamped oscillator oscillates with decreasing amplitude.

Figure 13.29. A plot of position versus time for an underdamped oscillator. The oscillator oscillates with decreasing amplitude in each cycle. The peaks and troughs of the cycles fall on exponential envelops, ash shown by dashed lines above and below, due to the exponential multiplicative factor \(\exp(-\gamma t /2) \) in the solution. Following values wer used to generate the plot: \(x_0=1\text{,}\) \(v_0=0\text{,}\) \(m=1\text{,}\) \(k=1\text{,}\) \(b = 0.05\text{.}\)

Subsection 13.8.4 Overdamped Solution

The overdamped solution shows only the exponential damping and no oscillations as illustrated in Figure 13.30. The solution consists of two terms that decay at different rates.

\begin{equation} x(t) = A\,e^{-a\, t} + B\,e^{-b\, t},\tag{13.57} \end{equation}

where, \(a \) and \(b\) are

\begin{align} \amp a = \dfrac{\gamma}{2} - \omega^{\prime\prime} , \tag{13.58}\\ \amp b = \dfrac{\gamma}{2} + \omega^{\prime\prime}, \tag{13.59} \end{align}

where

\begin{equation*} \omega^{\prime\prime} = \sqrt{ \left( \frac{\gamma}{2} \right)^2 - \omega^2 }. \end{equation*}

Since \(\dfrac{\gamma}{2} \gt \omega \gt \omega^{\prime\prime} \) for overdamping, both \(a \) and \(b\) are positive numbers.

Figure 13.30. A plot of position versus time for an overdamped oscillator. There are no cycles of oscillation in an overdamped oscillator. Following values wer used to generate the plot: \(x_0=1\text{,}\) \(v_0=0\text{,}\) \(m=1\text{,}\) \(k=1\text{,}\) \(b = 4.0\text{.}\)

Subsection 13.8.5 Critically Damped Solution

The critically damped solution shows a combination of exponential damping and a linearly increasing solution that is also damped exponentially. That means there is no oscillation here either.

\begin{equation} x(t) = A\,e^{-\gamma t / 2} + B\, t\, e^{-\gamma t / 2}.\tag{13.60} \end{equation}

Figure 13.32 illustrates critically damped oscillator. Visually, critically damped and overdamped oscillators appear similar, but when you plot the overdamped and critically damped oscillators under same initial conditions, as in Figure 13.32, you would find that critically damped oscillator does a little better job of damping the motion.

Figure 13.31. A plot of position versus time for an overdamped oscillator. There are no cycles of oscillation in an overdamped oscillator. Following values wer used to generate the plot: \(x_0=1\text{,}\) \(v_0=0\text{,}\) \(m=1\text{,}\) \(k=1\text{,}\) \(b = 2.0\text{.}\)

A very important application of critically damped oscillation is in car shock absorbers. A shock absorber provides critical damping to the springs of the suspension system and damps a car’s motion smoothly and rapidly. Without a shock absorber, a car ride would be very bumpy and dangerous. The picture to the right is a rear shock absorber and spring of a BMW R75/5 motorcycle, where the shock absorber is in the inside space of the spring (Photo credits: uploaded by Jeff Dean for Wikicommons.)

Figure 13.32. A plot of position versus time for three damped oscillators with the same initial conditions, \(x_0 = 1\) and \(v_0 = 1\text{.}\) The oscillators have \(m=1\text{,}\) \(k=1\text{,}\) but \(b\) is chosen different for the three - for underdamped, \(b = 0.5\text{,}\) for critically damped, \(b = 2 \text{,}\) and for overdamped, \(b = 4\text{.}\) The critically damped oscillator is seen to damp the motion better than the others.

Exercises 13.8.6 Exercises

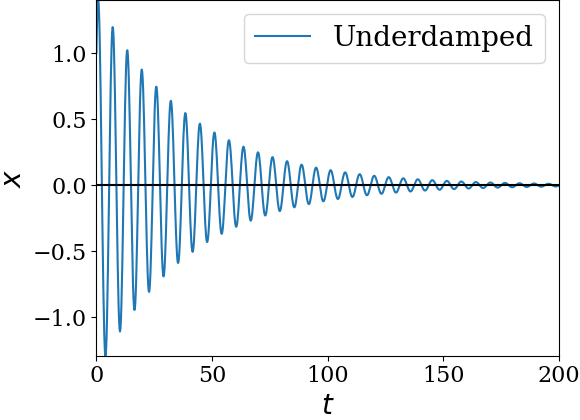
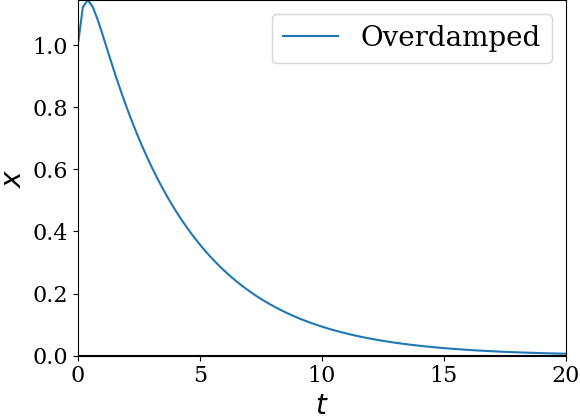
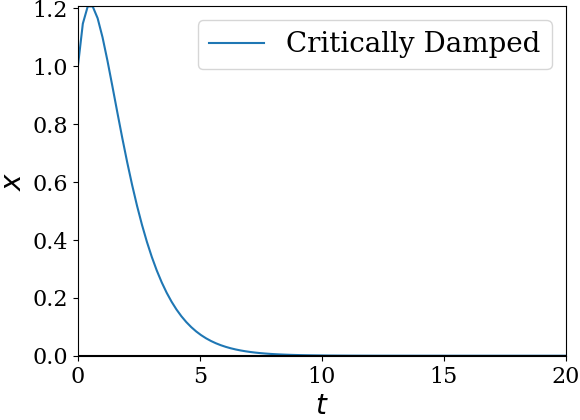
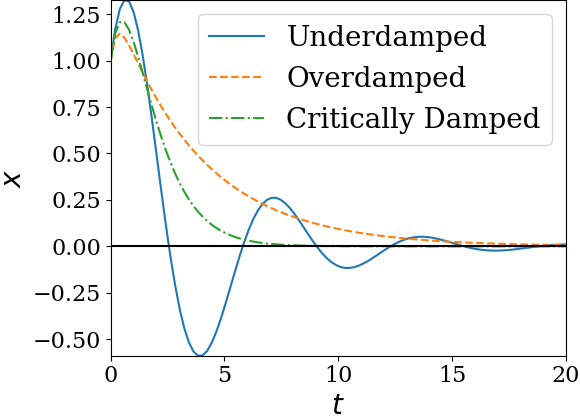
1. Deciding Type of Damped Harmonic Oscillator.

Decide what type of damping is in the following oscillators.

\begin{align*} \amp (a)\ \ m=0.2\text{ kg},\ k=10\text{ N/m},\ b=6\text{ kg/s}, \\ \amp (b)\ \ m=0.2\text{ kg},\ k=20\text{ N/m},\ b=8\text{ kg/s}, \\ \amp (c)\ \ m=0.8\text{ kg},\ k=32\text{ N/m},\ b=8\text{ kg/s}, \\ \amp (d)\ \ m=0.8\text{ kg},\ k=80\text{ N/m},\ b=16\text{ kg/s}, \end{align*}

Hint.

(a)-(d) First work out the effective parameters \(\omega\) and \(\gamma\text{.}\)

Answer.

(a) Overdamped, (b) Overdamped, (c) Underdamped, (d) Critically damped.

Solution 1. (a)

Let us first find the two effective parameters.

\begin{align*} \omega \amp = \sqrt{\dfrac{k}{m}} = \sqrt{\dfrac{10}{0.2}} = 7.07\text{ sec}^{-1}. \\ \gamma \amp = \dfrac{b}{m} = \dfrac{6}{0.2} = 30\text{ sec}^{-1}. \end{align*}

Since \(\omega \lt \gamma/2\text{,}\) the oscillator is overdamped.

Solution 2. (b)

Let us first find the two effective parameters.

\begin{align*} \omega \amp = \sqrt{\dfrac{k}{m}} = \sqrt{\dfrac{20}{0.2}} = 10.0\text{ sec}^{-1}. \\ \gamma \amp = \dfrac{b}{m} = \dfrac{8}{0.2} = 40\text{ sec}^{-1}. \end{align*}

Since \(\omega \lt \gamma/2\text{,}\) the oscillator is overdamped.

Solution 3. (c)

Let us first find the two effective parameters.

\begin{align*} \omega \amp = \sqrt{\dfrac{k}{m}} = \sqrt{\dfrac{32}{0.8}} = 6.32\text{ sec}^{-1}. \\ \gamma \amp = \dfrac{b}{m} = \dfrac{8}{0.8} = 10\text{ sec}^{-1}. \end{align*}

Since \(\omega \gt \gamma/2\text{,}\) the oscillator is underdamped.

Solution 4. (d)

Let us first find the two effective parameters.

\begin{align*} \omega \amp = \sqrt{\dfrac{k}{m}} = \sqrt{\dfrac{80}{0.8}} = 10.0\text{ sec}^{-1}. \\ \gamma \amp = \dfrac{b}{m} = \dfrac{16}{0.8} = 20\text{ sec}^{-1}. \end{align*}

Since \(\omega = \gamma/2\text{,}\) the oscillator is critically damped.

2. Lightly Damped Oscillator Solution and Envelop.

The position of a 250-gram lightly damped oscillator is given by the following function of time, \(x(t) = 2\exp{(-0.01\,t)}\cos(4\pi t)\text{,}\) where \(t\) is in seconds and \(x\) in meters.

(a) What is the frequency of oscillations?

(b) Plot \(x\) vs \(t\) for at least 4 cycles.

(d) How long does it take the envelop to drop by a factor \(\dfrac{1}{e^2}\text{?}\)

Hint.

(a) Look at the argument of the cosine. (b) plot \(t=0 \) to \(t=2\text{.}\) (c) Set \(0.01\, t = 1\text{.}\) (d) Set \(0.01\, t = 2\text{.}\)

Answer.

(a) \(2\text{ Hz}\text{,}\) (b) See solution, (c) \(100\text{ sec}\text{,}\) (d) \(200\text{ sec}\text{.}\)

Solution 1. (a)

From the argument of the cosine we can find the period of oscillations. The inverse of this period is the frequency. The period of \(\cos(4\pi t)\) is \(T= 0.5\text{ sec}\text{.}\) Hence, the frequency of the underdamped oscillatory is

\begin{equation*} f = \dfrac{1}{T} = 2\text{ Hz}. \end{equation*}

Solution 2. (b)

Plot the given function for the range \(t=[0,\ 2]\text{.}\)

Solution 3. (c)

The envelop is dropping in time as \(\exp{(-0.01\,t)}\text{.}\) We need to find the value of \(t\) at which the value becomes \(\exp{(-1)}\text{.}\) This means

\begin{equation*} 0.01\,t = 1\ \ \Longrightarrow\ \ t = 100\text{ sec}. \end{equation*}

Solution 4. (d)

The envelop is dropping in time as \(\exp{(-0.01\,t)}\text{.}\) We need to find the value of \(t\) at which the value becomes \(\exp{(-2)}\text{.}\) This means

\begin{equation*} 0.01\,t = 2\ \ \Longrightarrow\ \ t = 200\text{ sec}. \end{equation*}

3. Displacement of a Harmonic Oscillator Given Initial Displacement and Velocity.

A block of mass \(2\text{ kg}\) is attached to a spring of spring constant \(32\text{ N/m}\) is oscillating with damping constant \(8\text{ kg/s}\text{.}\) The block started at \(x = 2\text{ cm}\) from rest. Where is the block at an arbitrary instant \(t\text{?}\)

Hint.

First find out what type of damping it is and then use the general solution for \(x\) and \(v\) to fit the initial condition given.

Answer.

\(3.1\text{ cm}\,\exp(-4 t)\,\cos(\sqrt{12} t -0.86)\text{.}\)

Solution.

We have three formulas for \(x\) to choose from, depending upon the type of damping. The effective parameters are

\begin{align*} \omega \amp =\sqrt{\dfrac{32}{2}} = 4\text{ sec}^{-1},\\ \gamma \amp = \dfrac{8}{2} = 4\text{ sec}^{-1}. \end{align*}

Since \(\omega \gt \gamma/2\text{,}\) the damping is an underdamping with oscillation angular frequency

\begin{equation*} \omega^\prime = \sqrt{\omega^2 - \gamma^2/4 } = \sqrt{12}\text{ sec}^{-1}, \end{equation*}

and \(x\) and \(v\) as:

\begin{align*} x\amp = A\,\exp(-\gamma t)\,\cos(\omega^\prime t + \phi) \\ v\amp = -\gamma A\,\exp(-\gamma t)\,\cos(\omega^\prime t + \phi) -\omega^\prime A\,\exp(-\gamma t)\,\sin(\omega^\prime t + \phi) \end{align*}

Now, we use the given initial conditions to get

\begin{align*} 2\amp = A\, \cos\,\phi \\ 0\amp = -\gamma A\,\cos\,\phi -\omega^\prime A\,\sin\, \phi \end{align*}

The second equation gives \(\phi=-0.857\text{ rad}\) which is used in the first to get \(A=3.1\text{ cm}\text{.}\)

\begin{equation*} A = 3.1\text{ cm},\ \ \ \phi=-0.857. \end{equation*}

Therefore, we have the following \(x\) at arbitrary instant.

\begin{align*} x\amp = 3.1\text{ cm}\,\exp(-4 t)\,\cos(\sqrt{12} t -0.857), \end{align*}

where \(t\) is in \(\text{sec}\text{.}\)

4. Solving a Damped Oscillatory Problem Given Parameters and Initial Conditions.

A damped oscillator has following parameters \(m\) = 0.2 kg, \(k\) = 10 N/m, \(b\) = 6 kg/s. Suppose the oscillator moves on the \(x\)-axis with initial position and velocity values \(x(0) = 1\,\text{cm}\text{,}\) and \(v_x(0) = 0\text{.}\) Find \(x(t)\text{.}\)

Answer.

\(x(t) = -(0.068\ \textrm{cm})\ e^{-28 t} + (1.07\ \textrm{cm}) e^{-1.8 t}.\)

Solution.

Since this is a damped oscillator, we first need to knwo what type of dfamping is applicable here since the form of \(x(t)\) will depend on that. To decide the type, we need the values of \(\sqrt{k/m}\) and \(b/2m\text{.}\)

\begin{align*} \amp \omega_0 = \sqrt{k/m} = \sqrt{10/0.2} = \sqrt{50} = 7.1\,\text{s}^{-1}.\\ \amp \beta = \gamma/2 = \frac{b}{2m} = \frac{6}{2\times 0.2} = 15\,\text{s}^{-1}. \end{align*}

We see that \(\omega_0 \lt \gamma/2\text{.}\) Hence, it an overdamped oscillator. Therefore, \(x(t)\) will have form of the over-damped solution.

\begin{equation*} x(t) = e^{(-\beta t)}\ [ A\ e^{(-\alpha t)} + B\ e^{(\alpha t)}], \end{equation*}

where \(\beta = 15\ \textrm{s}^{-1}\) and \(\alpha = \sqrt{15^2-7.1^2} = 13.2\,\text{s}^{-1}\) . From this we get

\begin{equation*} v_x(t) = -(\alpha + \beta)A\ e^{[-(\alpha+\beta) t]} + (\alpha - \beta)B\ e^{[(\alpha-\beta) t]} . \end{equation*}

Now, we use the initial conditions on \(x\) and \(v_x\text{.}\)

\begin{align*} \amp 1 = A + B. \\ \amp 0 = -(\alpha + \beta) A + (\alpha - \beta)B. \end{align*}

Threfore,

\begin{align*} \amp A = \frac{\alpha - \beta}{2\alpha} = - 0.068\,\text{cm}\\ \amp B = \frac{\alpha + \beta}{2\alpha} = 1.07\,\text{cm}. \end{align*}

The solution

\begin{equation*} x(t) = -(0.068\ \textrm{cm})\ e^{-28 t} + (1.07\ \textrm{cm}) e^{-1.8 t}. \end{equation*}

5. Solving an Under Damped Oscillatory Problem Given Parameters and Initial Conditions.

A damped oscillator has following parameters \(m\) = 0.8 kg, \(k\) = 32 N/m, \(b\) = 8 kg/s. Suppose the oscillator moves on the \(x\)-axis with initial position and velocity values \(x(0) = 1\,\text{cm}\text{,}\) and \(v_x(0) = 0\text{.}\) Find \(x(t)\text{.}\)

Answer.

\(x(t) = e^{-5 t} \left[ 1\,\text{cm} \cos(6.3 t) + 0.79\,\text{cm}\sin(6.3 t) \right].\)

Solution.

\begin{align*} \amp \omega_0 = \sqrt{k/m} = \sqrt{32/0.8} = \sqrt{40} = 6.32\,\text{s}^{-1}.\\ \amp \beta = \gamma/2 = \frac{b}{2m} = \frac{8}{2\times0.8} =5 \,\text{s}^{-1}. \end{align*}

We see that \(\omega_0 \gt \gamma/2\text{.}\) Hence, it an underdamped oscillator. Therefore, \(x(t)\) will have form of the underdamped solution.

\begin{equation*} x(t) = e^{-\beta t} \left( A \cos\omega_1 t + B\sin\omega_1 t \right), \end{equation*}

where \(\beta = 5\ \textrm{s}^{-1}\) and \(\omega_1 = \sqrt{6.32^2-5^2} = 3.9 \,\text{s}^{-1}\) . From this we get

\begin{equation*} v_x(t) =-\beta e^{-\beta t} \left( A \cos\omega_1 t + B\sin\omega_1 t \right) + \omega_1 e^{-\beta t} \left( -A \sin\omega_1 t + B\cos\omega_1 t \right). \end{equation*}

Now, we use the initial conditions on \(x\) and \(v_x\text{.}\)

\begin{align*} \amp x(0) = 1\,\text{cm}\ \ \textrm{gives}\ \ 1\,\text{cm} = A \\ \amp v_x(0) = 0 \ \ \textrm{gives}\ \ 0 = -\beta A + \omega_1 B. \end{align*}

Therefore \(A = 1\,\text{cm}\) and \(B = \beta/\omega_1 = 0.79\,\text{cm}\text{.}\) Using these and the constants the solution for the given oscillator would be

\begin{equation*} x(t) = e^{-5 t} \left[ 1\,\text{cm} \cos(6.3 t) + 0.79\,\text{cm}\sin(6.3 t) \right]. \end{equation*}

Prev Top Next