Section 14.3 Polarization of Waves
The displacement from the equilibrium is often a vector property. The relative direction of the displacement and the direction of travel of wave defines the polarization of the wave.
If the displacements of particles of the medium happen perpendicular to the direction of travel of wave, e.g. when a rope is moved up and down at one end while the wave travels down the rope, we say that the wave is transversely polarized. In some waves, e.g., sound waves in air, the particles of air vibrate along the same axis as the wave travel. These types of waves are said to polarized longitudinally.
The longitudinal and transverse waves are easily demonstrated by waves on a slinky (Figure 14.9). Tie one end of a slinky to a post or ask a friend to hold it firmly. Hold the other end so that slinky is a little extended and taut.
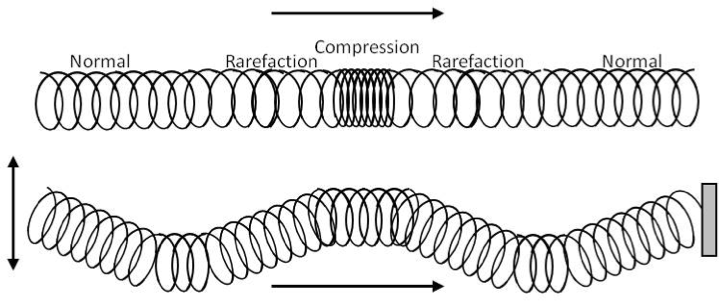
Now, you can set either a longitudinally polarized or a transversely polarized wave down the length of slinky. To get a longitudinally polarized wave, bunch a few turns together and let go, you will notice that the slinky winds and unwinds keeping the bunch shape of the disturbance more or less intact. To get a transversely polarized wave, pull one of the loops little to the right, left, up or down and let go. The transverse wave will travel down the slinky as it does for the rope described above.
In case of transversely polarized wave, the direction of polarization is in a plane perpendicular to the direction of propagation of the wave. That is, if the wave is traveling along the \(z\)-axis, the polarization direction will be in the \(xy\)-plane. The direction of polarization of a wave may change as wave travels or could remain fixed.
For instance of a transversely polarized wave in the \(xy\)-plane, polarization direction could be always pointed towards, say the \(x\)-axis or it could be towards \(x\)-axis at \((t,x)\) value and towards \(y\)-axis at another \((t,x)\) value. We will study these complications of polarization more fully when we study electromagnetic waves in the part on Optics.

